题目内容
(本小题满分12分)
某项计算机考试按科目A、科目B依次进行,只有大拿感科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目均合格方快获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率为 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为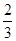 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这次考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为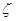 ,求随即变量
,求随即变量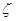 的分布列和数学期望.
的分布列和数学期望.
(1)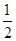
(2)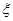
2 3 4 P 
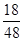
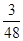
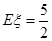
解析试题分析:设该人参加科目A考试合格和补考为时间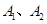 ,参加科目B考试合格和补考合格为时间
,参加科目B考试合格和补考合格为时间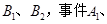
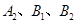 相互独立.
相互独立.
(1)设该人不需要补考就可获得证书为事件C,则C=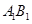 ,
,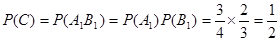 .
.
(2)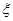 的可能取值为2,3,4. 则
的可能取值为2,3,4. 则
P(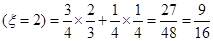 ;
;
P ;
;
P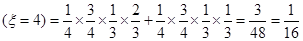 .
.
所以,随即变量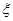 的分布列为
的分布列为
所以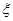
2 3 4 P 
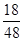
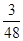
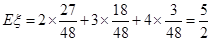 .
.
考点:离散型随机变量及其分布列;离散型随机变量的期望与方差.
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查学生分析问题和计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| | “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为
 ,其中
,其中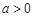 ,
,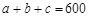 。当数据
。当数据 的方差
的方差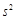 最大时,写出
最大时,写出 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时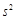 的值.
的值.(注:
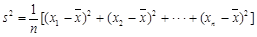 ,其中
,其中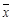 为数据
为数据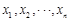 的平均数)
的平均数)  袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
. ;
; 为落入
为落入 的概率和
的概率和 .
.
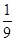 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为 ,试写出
,试写出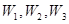 ,物理、化学、生物获得等级不是A的事件分别记为
,物理、化学、生物获得等级不是A的事件分别记为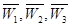 .
.