题目内容
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求直线B1C1与平面A1BC1所成角的正弦值;
(2)在线段BC1上确定一点D,使得AD⊥A1B,并求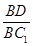 的值.
的值.
(1)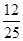 (2)
(2)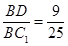
解析试题分析:(1)解决这类问题的思路是,根据几何体的结构特征找出或作出所求的线面角,再设法利用三角形知识求其正弦;或是建立适当的空间直角坐标系,借助法向量和直线的方向向量求直线与平面所成角的正弦;由于该问题中的几何体中棱的垂直关系较为明显,可采用后者.
(2)在(1)中已建立空间直角坐标系的基础上,用向量法解决垂直问题很是方便.
设D(x,y,z)是线段BC1上一点,且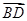 =λ
=λ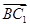 (λ∈[0,1]),求出向量
(λ∈[0,1]),求出向量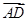 的坐标,利用互相垂直的向量的数量积为零建立方程,求出
的坐标,利用互相垂直的向量的数量积为零建立方程,求出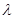 的值.
的值.
试题解析:(1)∵AA1C1C为正方形,∴AA1⊥AC.
∵平面ABC⊥平面AA1C1C,
∴AA1⊥平面ABC,
∴AA1⊥AC,AA1⊥AB.
由已知AB=3,BC=5,AC=4,∴AB⊥AC.
如图,以A为原点建立空间直角坐标系A-xyz,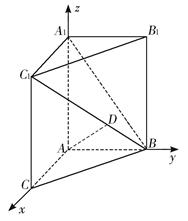
则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
∴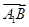 =(0,3,-4),
=(0,3,-4),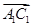 =(4,0,0),
=(4,0,0),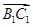 =(4,-3,0).
=(4,-3,0).
设平面A1BC1的法向量为n=(x,y,z),则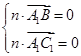 即
即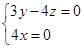
令z=3,则x=0,y=4,∴n=(0,4,3).
设直线B1C1与平面A1BC1所成的角为θ,则
sinθ=|cos<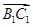 ,n>|=
,n>|=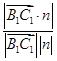 =
=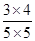 =
=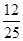 .
.
故直线B1C1与平面A1BC1所成角的正弦值为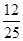 . 6分
. 6分
(2)设D(x,y,z)是线段BC1上一点,且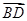 =λ
=λ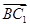 (λ∈[0,1]),
(λ∈[0,1]),
∴(x,y-3,z)=λ(4,-3,4),
∴x=4λ,y=3-3λ,z=4λ,
∴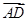 =(4λ,3-3λ,4λ).
=(4λ,3-3λ,4λ).
又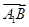 =(0,3,-4),
=(0,3,-4),
由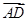 ·
·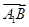 =0,得3(3-3λ)-4×4λ=0,
=0,得3(3-3λ)-4×4λ=0,
即9-25λ=0,解得λ=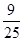 ∈[0,1].
∈[0,1].
故在线段BC1上存在点D,使得AD⊥A1B.
此时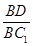 =λ=
=λ=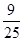 . 12分
. 12分
考点:1、直线与平面所成角的概念;2、空间直角坐标系;3、空间向量的夹角公式的应用.


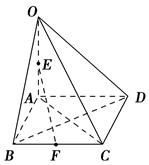
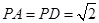 ,
,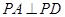 ,底面
,底面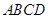 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 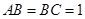 ,O为AD中点.
,O为AD中点.
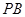 与平面
与平面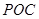 所成角的余弦值;
所成角的余弦值;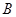 点到平面
点到平面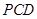 的距离;
的距离;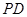 上是否存在一点
上是否存在一点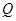 ,使得二面角
,使得二面角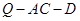 的余弦值为
的余弦值为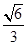 ?若存在,求出
?若存在,求出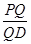 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.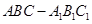 中,点
中,点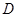 是
是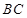 上一点.
上一点.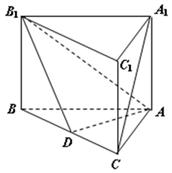
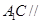 平面
平面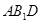 ;
;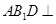 平面
平面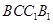 ,求证
,求证 .
. 中,
中,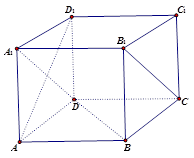
 ;
;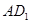 与直线BD所成的角
与直线BD所成的角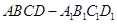 ,点
,点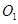 为
为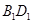 的中点.
的中点.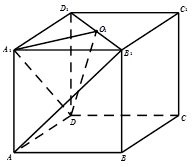
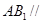 面
面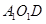 ;
;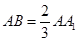 ,试问在线段
,试问在线段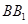 上是否存在点
上是否存在点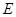 使得
使得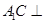
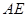 ,若存在求出
,若存在求出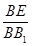 ,若不存在,说明理由.
,若不存在,说明理由.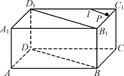
 ,这样的直线有几条,应该如何作图?
,这样的直线有几条,应该如何作图?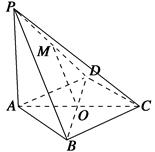
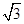 时,求PB的长.
时,求PB的长.