题目内容
18.已知a,b,c∈R+,且满足$\frac{kabc}{a+b+c}$≤(a+b)2+(a+b+4c)2,求k的最大值.分析 运用均值不等式,对不等式的右边变形,再将a+b+c乘到右边,除以abc,拆成五项的和相乘,再由均值不等式,即可得到最小值,可得k的最大值.
解答 解:由均值不等式得,(a+b)2+(a+b+4c)2=(a+b)2+[(a+2c)+(b+2c)]2
≥[2$\sqrt{ab}$]2+[2$\sqrt{2ac}$+2$\sqrt{2bc}$)]2=4ab+8ac+8bc+16c$\sqrt{ab}$,
于是$\frac{[(a+b)^{2}+(a+b+4c)^{2}](a+b+c)}{abc}$≥$\frac{(4ab+8ac+8bc+16c\sqrt{ab})(a+b+c)}{abc}$
=($\frac{4}{c}$+$\frac{8}{b}$+$\frac{8}{a}$+$\frac{16}{\sqrt{ab}}$)(a+b+c)
=8($\frac{1}{2c}$+$\frac{1}{b}$+$\frac{1}{a}$+$\frac{1}{\sqrt{ab}}$+$\frac{1}{\sqrt{ab}}$)($\frac{a}{2}$+$\frac{a}{2}$+$\frac{b}{2}$+$\frac{b}{2}$+c)
≥8•5•$\root{5}{\frac{1}{2c{a}^{2}{b}^{2}}}$•5•$\root{5}{\frac{{a}^{2}{b}^{2}c}{16}}$=100.
∴当且仅当a=b=2c>0时取最小值,
由题意可得k≤$\frac{[(a+b)^{2}+(a+b+4c)^{2}](a+b+c)}{abc}$恒成立.
即有k≤100.
故k的最大值为100.
点评 本题考查函数的最值的求法,注意运用均值不等式,以及满足的条件:一正二定三等,具有一定的技巧,属于难题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
| A. | $(-∞,\frac{1}{4}]$ | B. | $(-\frac{3}{4},+∞)$ | C. | $[-\frac{3}{4},\frac{1}{4}]$ | D. | $(-1,\frac{1}{4}]$ |
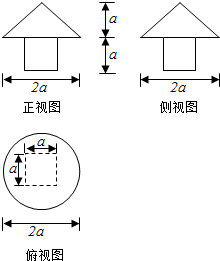 一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.
一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.