题目内容
一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,继续再取一个零件,直到取得正品为止.设取得正品之前已取出的次品数为ξ,求ξ的分布列及ξ的期望.
解:显然ξ所有可能取的值为0,1,2,3.
∵P(ξ=0)= ,
,
P(ξ=1)=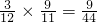 ,
,
P(ξ=2)= ,
,
P(ξ=3)= ,
,
∴ξ的分布列是:
∴Eξ=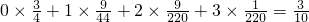 .
.
分析:ξ所有可能取的值为0,1,2,3,P(ξ=0)= ,P(ξ=1)=
,P(ξ=1)=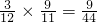 P(ξ=2)=
P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.
点评:本题考查离散型随机变量的分布列和数学期望,是基础题.解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.
∵P(ξ=0)=
 ,
,P(ξ=1)=
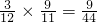 ,
,P(ξ=2)=
 ,
,P(ξ=3)=
 ,
,∴ξ的分布列是:
| ζ | 0 | 1 | 2 | 3 |
| P |  | 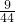 |  |  |
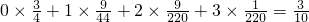 .
.分析:ξ所有可能取的值为0,1,2,3,P(ξ=0)=
 ,P(ξ=1)=
,P(ξ=1)=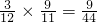 P(ξ=2)=
P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.点评:本题考查离散型随机变量的分布列和数学期望,是基础题.解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目