题目内容
一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,再取一个零件,直到取得正品为止.求在取得正品之前已取出次品数的期望.
解:设取得正品之前已取出的次品数为ξ,显然ξ所有可能取的值为0,1,2,3
当ξ=0时,即第一次取得正品,试验停止,则
P(ξ=0)=
当ξ=1时,即第一次取出次品,第二次取得正品,试验停止,则
P(ξ=1)=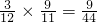
当ξ=2时,即第一、二次取出次品,第三次取得正品,试验停止,则
P(ξ=2)=
当ξ=3时,即第一、二、三次取出次品,第四次取得正品,试验停止,则
P(ξ=3)=
所以,Eξ=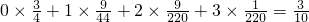
分析:首先分析题目求在取得正品之前已取出次品数的期望,需要求得在取得正品之前已取出次品数的分布,故需要分类讨论取出次品数分布为0,1,2,3的概率,再由期望公式即可求得结果.
点评:此题主要考查离散型随机变量的期望和方差,以及学生在实际问题的求解能力,需要分类讨论,属于中档题目.
当ξ=0时,即第一次取得正品,试验停止,则
P(ξ=0)=

当ξ=1时,即第一次取出次品,第二次取得正品,试验停止,则
P(ξ=1)=
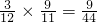
当ξ=2时,即第一、二次取出次品,第三次取得正品,试验停止,则
P(ξ=2)=

当ξ=3时,即第一、二、三次取出次品,第四次取得正品,试验停止,则
P(ξ=3)=

所以,Eξ=
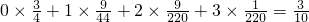
分析:首先分析题目求在取得正品之前已取出次品数的期望,需要求得在取得正品之前已取出次品数的分布,故需要分类讨论取出次品数分布为0,1,2,3的概率,再由期望公式即可求得结果.
点评:此题主要考查离散型随机变量的期望和方差,以及学生在实际问题的求解能力,需要分类讨论,属于中档题目.

练习册系列答案
相关题目