题目内容
下列极限正确的个数是( )
①
=0(α>0);
②
qn=0;
③
=-1;
④
C=C(C为常数).
①
| lim |
| n→∞ |
| 1 |
| nα |
②
| lim |
| n→∞ |
③
| lim |
| n→∞ |
| 1-2n |
| 2n+1 |
④
| lim |
| n→∞ |
| A、2 | B、3 | C、4 | D、都不正确 |
分析:由
qn=
知②不正确.由极限的概念知①③④成立.
| lim |
| n→∞ |
|
解答:解:①n→∞,nα→∞,
→∞,∴
=0(α>0),故①正确.
②
qn=
,由此可知②不正确.其它三个都正确.
③
=
=-1,故③成立.
④
C=C(C为常数).显然成立.
故选B.
| 1 |
| nα |
| lim |
| n→∞ |
| 1 |
| nα |
②
| lim |
| n→∞ |
|
③
| lim |
| n→∞ |
| 1-2n |
| 2n+1 |
| lim |
| n→∞ |
| ||
1+
|
④
| lim |
| n→∞ |
故选B.
点评:本题考查极限的概念,解题要认真审题,仔细解答.

练习册系列答案
相关题目
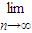
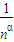 =0(α>0);
=0(α>0);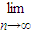 qn=0;
qn=0;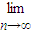
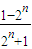 =-1;
=-1;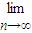 C=C(C为常数).
C=C(C为常数).