题目内容
16.连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
16.②③⑤
解析:如下图,对于斜率为k(k≠0)的一组平行线均可与抛物线有两个交点,取其中任意两条线构成四边形ABCD,显然AD∥BC,但由抛物线性质知,AB与CD不平行,故ABCD不可能为平行四边形,同时也不可能为菱形.
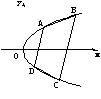
又∵AD∥BC,∴ABCD为梯形.
故①④不可能是,而③可能是.
由上图知,当四边形边AD确定时,过A总可以作弦AB使AB=AD.
同样可做出CD=AD.
∴可能是有三边相等的四边形.
故②可能是.
如下图,总有直线l与抛物线交于A、B两点,作弦AB的垂直平分线交抛物线与C、D两点,连结AC、BC、AD、BD,根据垂直平分线的性质,AC=BC且AD=BD,故∠CAB=∠CBA,且∠DAB=∠DBA.
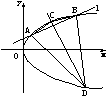
∴∠CAD=∠CBD,
即四边形ACBD对角相等.
故⑤可能是.

练习册系列答案
相关题目