题目内容
已知-
<θ<
,且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,在以下四个答案中,可能正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、-3 | ||
B、3或
| ||
C、-
| ||
D、-3或-
|
分析:由θ的范围,得到cosθ大于0,把已知的等式两边平方,利用同角三角函数间的基本关系化简后,由a的范围得到2sinθcosθ的值大于0,进而得到sinθ的值小于0,又根据sinθ+cosθ=a,a大于0,得到cosθ>-sinθ>0,再利用不等式的基本性质及同角三角函数间的基本关系化简,得到tanθ值的范围,即可判断出符合题意的tanθ值的可能值.
解答:解:由-
<θ<
,得到cosθ>0,
所以把sinθ+cosθ=a两边平方得:
(sinθ+cosθ)2=a2,
即sin2θ+cos2θ+2sinθcosθ=1+2sinθcosθ=a2,又a∈(0,1),
所以2sinθcosθ=a2-1<0,所以sinθ<0,
又sinθ+cosθ=a>0,
所以cosθ>-sinθ>0,
则-1<tanθ<0.
故选C
| π |
| 2 |
| π |
| 2 |
所以把sinθ+cosθ=a两边平方得:
(sinθ+cosθ)2=a2,
即sin2θ+cos2θ+2sinθcosθ=1+2sinθcosθ=a2,又a∈(0,1),
所以2sinθcosθ=a2-1<0,所以sinθ<0,
又sinθ+cosθ=a>0,
所以cosθ>-sinθ>0,
则-1<tanθ<0.
故选C
点评:此题考查了同角三角函数间的基本关系,要求学生掌握余弦函数的图象与性质,不等式的基本性质,以及同角三角函数间的基本关系,解本题的思路是利用同角三角函数间的基本关系及不等式的基本性质求出tanθ的范围.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
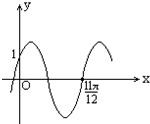
已知如图是函数y=2sin(ωx+φ)(|φ|<
)的图象,那么( )
| π |
| 2 |

A、?=
| ||||
B、?=
| ||||
C、?=2,φ=
| ||||
D、?=2,φ=-
|