题目内容
(本小题满分10分)选修4—1:几何证明选讲
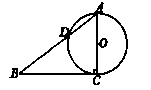
已知⊙O的弦AB长为4,将线段AB延长到点P,使BP = 2;过点P作直线PC切⊙O于点C;
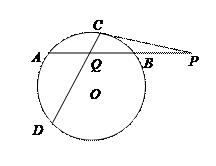
(1)求线段PC的长;
(2)作⊙O的弦CD 交AB于点Q(CQ<DQ),且Q为AB中点,又CD =
交AB于点Q(CQ<DQ),且Q为AB中点,又CD =  5,求线段CQ的长。
5,求线段CQ的长。
已知⊙O的弦AB长为4,将线段AB延长到点P,使BP = 2;过点P作直线PC切⊙O于点C;

(1)求线段PC的长;
(2)作⊙O的弦CD
 交AB于点Q(CQ<DQ),且Q为AB中点,又CD =
交AB于点Q(CQ<DQ),且Q为AB中点,又CD =  5,求线段CQ的长。
5,求线段CQ的长。解:(1)由切割线定理:PC2=PA·PB=(2+4)×2=12。所以PC=2。(4分)
(2)由相交弦定理:CQ·QD=AQ·QB,所以CQ(5-CQ)=4,得:CQ2-5CQ+4=0,
解得:CQ=5(舍去)或CQ=1,所以CQ的长为1。(10分)

(2)由相交弦定理:CQ·QD=AQ·QB,所以CQ(5-CQ)=4,得:CQ2-5CQ+4=0,
解得:CQ=5(舍去)或CQ=1,所以CQ的长为1。(10分)
略

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 是圆
是圆 的直径,
的直径, 在
在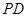 切圆
切圆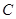 .已知圆
.已知圆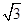 ,
,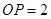 ,则
,则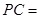 ______;
______;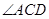 的大小为______.
的大小为______.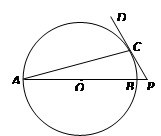
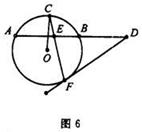
 若BE=1,DE=2AE,求DF的长.
若BE=1,DE=2AE,求DF的长.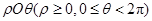 中,点
中,点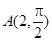 关于直线
关于直线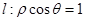 的对称点的极坐标为 .
的对称点的极坐标为 . 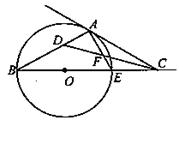
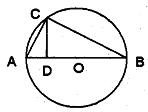
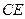 与⊙O的交点.若
与⊙O的交点.若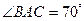 ,则
,则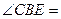 ______;若
______;若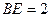 ,
,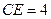 ,则
,则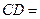 .
.
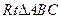 的两条直角边
的两条直角边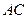 ,
,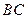 的长分别为
的长分别为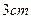 ,
,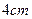 ,以
,以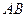 交于点
交于点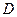 ,则
,则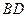 =
= 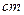 .
.
 是半圆
是半圆 的直径,点
的直径,点 在
在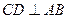 ,垂足为
,垂足为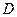 ,且
,且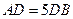 ,设
,设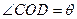 ,
,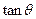 的值为 .
的值为 .