题目内容
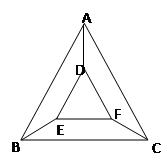
如图,用五种不同的颜色给图中的A、B、C、D、E、F六个不同的点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共( )种。
A、1240 B、360 C、1920 D、264

A、1240 B、360 C、1920 D、264
C
试题分析:由于A和E或F可以同色、B和D或F可以同色、C和D或E可以同色,所以当五种颜色都选择时,选法有
 种;当五种颜色选择4种时,选法有
种;当五种颜色选择4种时,选法有 种;当五种颜色选择3种时,选法有
种;当五种颜色选择3种时,选法有 种,所以不同的涂色方法共
种,所以不同的涂色方法共 。故选C。
。故选C。点评:关于排列和组合的问题,常要分情况讨论,像本题,要分着五种、四种和三种颜色。

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
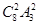
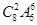
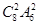
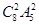

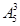
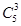
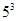
 19中国旅游 日庆典活动”的志愿者,要求既有男生又有女生,且男生甲和女生乙至多只能一人参加,则不同的选派方法有 种(用数作答).
19中国旅游 日庆典活动”的志愿者,要求既有男生又有女生,且男生甲和女生乙至多只能一人参加,则不同的选派方法有 种(用数作答).



 ,则
,则 的值为 .
的值为 .