题目内容
（09年滨州一模文）（14分）
已知直线
所经过的定点
恰好是椭圆
的一个焦点,且椭圆上的点到点的最大距离为8.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）已知圆
,直线
.试证明：当点
在椭圆上运动时，直线
与圆
恒相交，并求直线被圆所截得弦长
的取值范围.
解析:（Ⅰ）由
得，
，
所以直线过定点（3，0），即
. …………………2分
设椭圆
的方程为
,
则
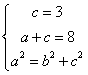,解得
，
所以椭圆的方程为
. ……………………5分
（Ⅱ）因为点
在椭圆上运动,所以
， ………………6分
从而圆心
到直线
的距离
所以直线
与圆恒相交. ……………………9分
又直线被圆截得的弦长
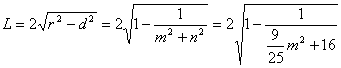， …………12分
由于
,所以
,则
,
即直线被圆截得的弦长的取值范围是. …………………14分
练习册系列答案
相关题目
上的函数
在区间
上的最大值是5，最小值是－11.
的解析式；
时，
恒成立，求实数
的取值范围.
中，
、
、
两两互相垂直，且
，
,
、
分别为
、
的中点.
平面
；
平面
；
的体积.
、
、
分别为
的三边
、
、
所对的角，向量
，
，且
.
，
，
成等差数列，且
，求边（09年滨州一模文）（12分）
某高级中学共有学生2000人，各年级男、女生人数如下表：
| 高一 | 高二 | 高三 |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19.
（Ⅰ）现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少人？
（Ⅱ）已知
求高三年级女生比男生多的概率.