题目内容
已知函数y=asinx+bcosx+c的图象上有一个最低点(| 11 |
| 6 |
| 3 |
| π |
分析:先利用辅助角公式对函数化简可得,y=asinx+bcosx+c=
sin(x+?)+c,由(
π,1)是图象上的最低点可得取得最值的条件x=
及最小值为1即
,从而可求函数解析式再由f(x)=3的所有正根依次为一个公差为3的等差数列,可得曲线y=f(x)与直线y=3的相邻交点间的距离都相等,根据三角函数的图象与性质,即过f(x)的最高点或最低点,要么过曲线的拐点(平衡位置点),且由于(
π,1)是图象上的最低点,结合已知可求答案.
| a2+b2 |
| 11 |
| 6 |
| 11π |
| 6 |
|
| 11 |
| 6 |
解答: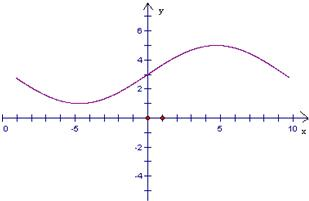 解:y=asinx+bcosx+c=
解:y=asinx+bcosx+c=
sin(x+?)+c,
其中φ满足tan?=
,φ与(a,b)同象限,
由于(
π,1)是图象上的最低点,所以
,
即
.所以y=(c-1)sin(x+2kπ-
π)+c=(c-1)sin(x-
)+c,
将上述图象上每点纵坐标不变,横坐标缩短到原来的
倍,
得y=(c-1)sin(
x-
)+c
然后向左平移1个单位可得y=(c-1)sin(
(x+1)-
)+cy=(c-1)sin
x+c,
所以f(x)=(c-1)sin
x+c,T=
=6.
由于f(x)=3的所有正根依次为一个公差为3的等差数列,
即曲线y=f(x)与直线y=3的相邻交点间的距离都相等,
根据三角函数的图象与性质,直线y=3要么与曲线y=f(x)相切,
即过f(x)的最高点或最低点,要么过曲线的拐点(平衡位置点),注意到(
π,1)是图象上的最低点,
故:当y=3与曲线y=f(x)在最高点相切时,即sin
x=1,f(x)=2c-1=3,
所以c=2,此时周期应为公差3,这将与上面已知周期为6矛盾.故舍去
当y=3过曲线y=f(x)拐点(平衡位置点)时,即sin
x=0,f(x)=c=3,
此时周期为6恰为公差3的2倍,符合题意.
所以f(x)=2sin
x+3,由2kπ+
≤
x≤2kπ+
π,k∈z,
得6k+
≤x≤6k+
,k∈z,y=f(x)单调减区间[6k+
,6k+
](k∈z),草图为:
 解:y=asinx+bcosx+c=
解:y=asinx+bcosx+c=| a2+b2 |
其中φ满足tan?=
| b |
| a |
由于(
| 11 |
| 6 |
|
即
|
| 7 |
| 3 |
| π |
| 3 |
将上述图象上每点纵坐标不变,横坐标缩短到原来的
| 3 |
| π |
得y=(c-1)sin(
| π |
| 3 |
| π |
| 3 |
然后向左平移1个单位可得y=(c-1)sin(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
所以f(x)=(c-1)sin
| π |
| 3 |
| 2π | ||
|
由于f(x)=3的所有正根依次为一个公差为3的等差数列,
即曲线y=f(x)与直线y=3的相邻交点间的距离都相等,
根据三角函数的图象与性质,直线y=3要么与曲线y=f(x)相切,
即过f(x)的最高点或最低点,要么过曲线的拐点(平衡位置点),注意到(
| 11 |
| 6 |
故:当y=3与曲线y=f(x)在最高点相切时,即sin
| π |
| 3 |
所以c=2,此时周期应为公差3,这将与上面已知周期为6矛盾.故舍去
当y=3过曲线y=f(x)拐点(平衡位置点)时,即sin
| π |
| 3 |
此时周期为6恰为公差3的2倍,符合题意.
所以f(x)=2sin
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
得6k+
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
点评:本题主要考查了辅助角公式的应用,三角函数的图象变换,三角函数与数列的综合,直线与曲线的关系等知识的综合运用,属于综合试题,要求考生具备一定的推理论证的能力.

练习册系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
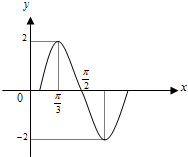 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数