题目内容
数列{an}满足: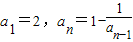 (n=2,3,4,…),若数列{an}有一个形如an=Asin(ωn+φ)+B的通项公式,其中A、B、ω、φ均为实数,且A>0,ω>0,|φ|<
(n=2,3,4,…),若数列{an}有一个形如an=Asin(ωn+φ)+B的通项公式,其中A、B、ω、φ均为实数,且A>0,ω>0,|φ|<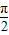 ,则an= .(只要写出一个通项公式即可)
,则an= .(只要写出一个通项公式即可)
【答案】分析:由题设得到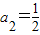 ,a3=-1,a4=2,因为数列有个形如an=Asin(ωn+φ)+B的通项公式,而数列的周期是3,所以
,a3=-1,a4=2,因为数列有个形如an=Asin(ωn+φ)+B的通项公式,而数列的周期是3,所以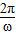 =3,ω=
=3,ω=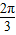 ,由此可以得到它的一个通项公式可以是an=3sin(
,由此可以得到它的一个通项公式可以是an=3sin( .
.
解答:解: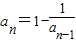 ,a1=2,由此得到
,a1=2,由此得到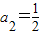 ,a3=-1,a4=2,
,a3=-1,a4=2,
因为数列有个形如an=Asin(ωn+φ)+B的通项公式,
而数列的周期是3,所以 =3,ω=
=3,ω=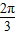 ,
,
代入得Asin(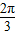 +φ)+B=2,Asin(
+φ)+B=2,Asin(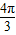 +φ)+B=
+φ)+B= ,Asin(2π+φ)+B=-1
,Asin(2π+φ)+B=-1
解得A=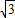 ,B=
,B= ,φ=-
,φ=-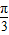 ,
,
所以其中一个通项公式可以是an=3sin( .
.
点评:本题考查数列的性质和应用,解题时要注意三角函数的应用.
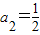 ,a3=-1,a4=2,因为数列有个形如an=Asin(ωn+φ)+B的通项公式,而数列的周期是3,所以
,a3=-1,a4=2,因为数列有个形如an=Asin(ωn+φ)+B的通项公式,而数列的周期是3,所以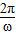 =3,ω=
=3,ω=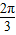 ,由此可以得到它的一个通项公式可以是an=3sin(
,由此可以得到它的一个通项公式可以是an=3sin( .
.解答:解:
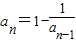 ,a1=2,由此得到
,a1=2,由此得到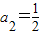 ,a3=-1,a4=2,
,a3=-1,a4=2,因为数列有个形如an=Asin(ωn+φ)+B的通项公式,
而数列的周期是3,所以
 =3,ω=
=3,ω=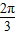 ,
,代入得Asin(
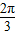 +φ)+B=2,Asin(
+φ)+B=2,Asin(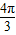 +φ)+B=
+φ)+B= ,Asin(2π+φ)+B=-1
,Asin(2π+φ)+B=-1解得A=
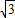 ,B=
,B= ,φ=-
,φ=-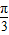 ,
,所以其中一个通项公式可以是an=3sin(
 .
.点评:本题考查数列的性质和应用,解题时要注意三角函数的应用.

练习册系列答案
相关题目