题目内容
打鼾不仅影响别人休息，而且可能与患某种疾病有关．下表是一次调查所得的数据，(1)将本题的2*2联表格补充完整。
(2)用提示的公式计算，每一晚都打鼾与患心脏病有关吗？
提示：
| | 患心脏病 | 未患心脏病 | 合计 |
| 每一晚都打鼾 | 3 | 17 | a = |
| 不打鼾 | 2 | 128 | b = |
| 合计 | c = | d = | n = |
（1）
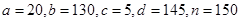（2）有99%的把握说“每一晚都打鼾与患心脏病有关”
解析试题分析：（1）由表中数据易求得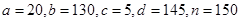
；
（2）公式相关指数公式计算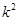
的观测值，根据临界值表判定“每一晚都打鼾与患心脏病有关”的可靠性.
试题解析：（1）由表中数据可得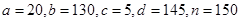
（2）由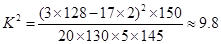
，
，
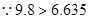有99%的把握说“每一晚都打鼾与患心脏病有关”.
考点：两个变量相关指数；独立检验方法.
练习册系列答案
相关题目
某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究，对该校高二年级800名学生上学期期 数学和化学成绩，按优秀和不优秀分类得结果：数学和化学都优秀的有60人，数学成绩优秀但化学不优秀的有140人，化学成绩优秀但数学不优秀的有100人．
（Ⅰ）补充完整表格并判断能否在犯错概率不超过0．001前提下认为该校学生的数学成绩与化学成绩有关系？
| | 数学优秀 | 数学不优秀 | 总计 |
| 化学优秀 | | | |
| 化学不优秀 | | | |
| 总计 | | | |
（Ⅱ）4名成员随机分成两组，每组2人，一组负责收集成绩，另一组负责数据处理。求学生甲分到负责收集成绩组，学生乙分到负责数据处理组的概率。
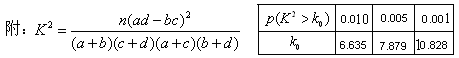
为了整顿道路交通秩序，某地考虑将对行人闯红灯进行处罚．为了了解市民的态度，在普通行人中随机选取了200人进行调查，得到如下数据：
处罚金额 （元） | 0 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 80 | 50 | 40 | 20 | 10 |
（Ⅰ）求这两种金额之和不低于20元的概率；
（Ⅱ）若用X表示这两种金额之和，求X的分布列和数学期望．
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下
| | 男 | 女 | 合计 |
| 需要 | 40 | 30 | |
| 不需要 | 160 | 270 | |
| 合计 | | | |
（2）能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关系?
（3）根据（2）的结论,能否提出更好的调查方法估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附表：
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
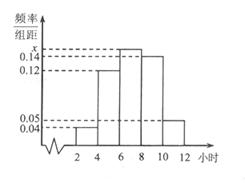
某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：
 | 2 | 3 | 4 | 5 | 6 |
 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
，
，(1)在下面坐标系中画出散点图；
(2)计算
，
，并求出线性回归方程；(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?
