题目内容
已知函数f(x)=x3+ax2+bx+c的图象经过原点,且在x=1处取得极值,直线y=2x+3到曲线y=f(x)在原点处的切线所成的角为45°.
(1)求f(x)的解析式;
(2)若对于任意实数α和β恒有不等式|f(2sinα)-f(2sinβ)|≤m成立,求m的最小值.
(1)解:由题意有f(0)=c=0,f'(x)=3x2+2ax+b且f′(1)=3+2a+b=0
又曲线y=f(x)在原点处的切线的斜率k=f′(0)=b,而直线y=2x+3到此切线所成的角为45°,
∴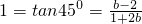 ,解得b=-3,代入f′(1)=3+2a+b=0得a=0,
,解得b=-3,代入f′(1)=3+2a+b=0得a=0,
∴f(x)=x3-3x….(6分)
(2)解:由f′(x)=3x2-3=3(x-1)(x+1)可知,f(x)在(-∞,-1]和[1,+∞)上递增,在[-1,1]上递减.
又f(-2)=-2,f(-1)=2,f(1)=-2,f(2)=2,
∴f(x)在[-2,2]上的最大值和最小值分别为-2和2,….(12分)
又∵sinα∈[-2,2],2sinβ∈[-2,2]
∴|f(2sinα)-f(2sinβ)|≤4
故m的最小值为4.….(15分)
分析:(1)由函数f(x)=x3+ax2+bx+c的图象经过原点,有f(0)=c=0,利用在x=1处取得极值可知f′(1)=3+2a+b=0
又曲线y=f(x)在原点处的切线的斜率k=f′(0)=b,而直线y=2x+3到此切线所成的角为45°,根据到角公式可求得解得b=-3,从而可求函数的解析式;
(2)由f′(x)=3x2-3=3(x-1)(x+1)可知,f(x)在(-∞,-1]和[1,+∞)上递增,在[-1,1]上递减,从而可得f(x)在[-2,2]上的最大值和最小值分别为-2和2,根据2sinα∈[-2,2],2sinβ∈[-2,2],可得m的最小值.
点评:本题以函数为载体,考查导数的几何意义,考查利用导数求函数的极值、最值.
又曲线y=f(x)在原点处的切线的斜率k=f′(0)=b,而直线y=2x+3到此切线所成的角为45°,
∴
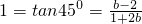 ,解得b=-3,代入f′(1)=3+2a+b=0得a=0,
,解得b=-3,代入f′(1)=3+2a+b=0得a=0,∴f(x)=x3-3x….(6分)
(2)解:由f′(x)=3x2-3=3(x-1)(x+1)可知,f(x)在(-∞,-1]和[1,+∞)上递增,在[-1,1]上递减.
又f(-2)=-2,f(-1)=2,f(1)=-2,f(2)=2,
∴f(x)在[-2,2]上的最大值和最小值分别为-2和2,….(12分)
又∵sinα∈[-2,2],2sinβ∈[-2,2]
∴|f(2sinα)-f(2sinβ)|≤4
故m的最小值为4.….(15分)
分析:(1)由函数f(x)=x3+ax2+bx+c的图象经过原点,有f(0)=c=0,利用在x=1处取得极值可知f′(1)=3+2a+b=0
又曲线y=f(x)在原点处的切线的斜率k=f′(0)=b,而直线y=2x+3到此切线所成的角为45°,根据到角公式可求得解得b=-3,从而可求函数的解析式;
(2)由f′(x)=3x2-3=3(x-1)(x+1)可知,f(x)在(-∞,-1]和[1,+∞)上递增,在[-1,1]上递减,从而可得f(x)在[-2,2]上的最大值和最小值分别为-2和2,根据2sinα∈[-2,2],2sinβ∈[-2,2],可得m的最小值.
点评:本题以函数为载体,考查导数的几何意义,考查利用导数求函数的极值、最值.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|