题目内容
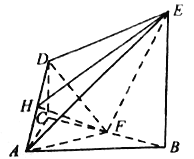
【题目】如图，在多面体ABCDE中，
，
平面ABC，
，
，F为BC的中点，且
.
（1）求证：
平面ADF；
（2）求二面角
的正切值.
【答案】（1）见解析；（2）
【解析】
（1）先证
，
，证AF⊥平面CDEB，得EF⊥AF，又EF⊥AD，从而EF⊥平面ADF；
（2）过点F作FH⊥AD，垂足为H，连接EH，可得∠EHF为二面角EADF的平面角，然后求出EF和FH，即可求出正切值．
解：（1）因为
平面ABC，所以，
因为
，F为BC的中点，
所以，又
，
所以
平面CDEB，
所以
，又因为
，且
，
所以
平面ADF.
（2）过点F作
，垂足为H，连接EH
由（1）知
，
所以
为二面角E-AD-F的平面角，
因为
，F为BC的中点，
所以
因为
，平面ABC，
所以
平面ABC，
，
所以
由（1）知
，所以
，
所以
，所以
因为
，
所以
，所以
，
因为平面CDEB，所以
，所以
由等面积法得
，
所以
，
所以二面角E-AD-F的正切值为.
练习册系列答案
相关题目
