题目内容
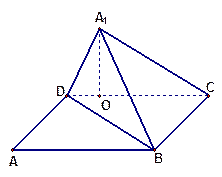
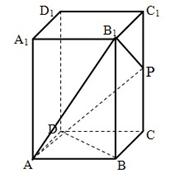
(12分)如图,等边 与直角梯形
与直角梯形 垂直,
垂直, ,
,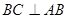 ,
,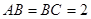 ,
,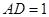 .若
.若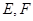 分别为
分别为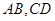 的中点.
的中点.
(1)求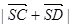 的值; (2)求面
的值; (2)求面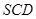 与面
与面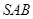 所成的二面角大小.
所成的二面角大小.
(1) ;
;
(2)面SCD与面SAB所成的二面角大小为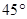 .
.
解析试题分析:(1)因为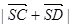
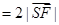 ,然后再在
,然后再在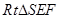 中求值即可.
中求值即可.
(2)利用空间向量法求二面角,要首先求出二面角两个面的法向量然后转化为两个面的法向量的夹角求解.
(1)在正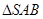 中
中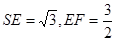 ,面
,面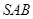
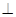 面
面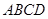 ,
,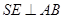
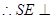 面
面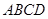 ,
,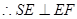 ,
,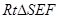 中,
中,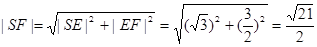
 (也可用坐标计算)………6分
(也可用坐标计算)………6分
(2)建立如图所示的直角坐标系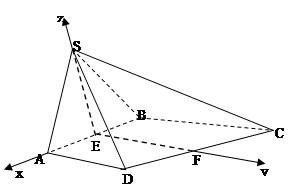
则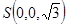 ,
,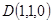 ,
,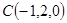
设面SCD的法向量为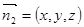
由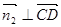
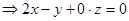 ,由
,由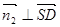
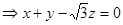
不妨设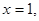 则
则 ,
,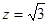 ,
,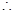
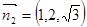 ,
,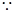 面SAB的法向量为
面SAB的法向量为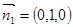
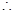
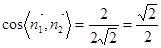
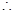 面SCD与面SAB所成的二面角大小为
面SCD与面SAB所成的二面角大小为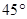 .
.
考点:空间几何体的线线,线面,面面垂直的判定与性质,向量的运算,二面角.
点评:(1)本小题在进行向量运算时用到的公式:若M为BC的中点,则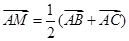 .
.
(2)在利用空间向量求二面角时首先求出两个面的法向量,同时要注意法向量的夹角与二面角可能相等也可能互补,要注意判断准确.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 中,
中, ,
, ,
, 的中点.
的中点.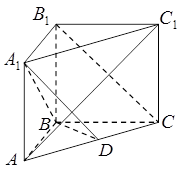
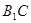 ∥
∥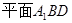 ;
;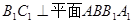 ;
;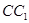 上是否存在一点
上是否存在一点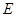 ,使得
,使得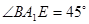 ,若存在,试确定
,若存在,试确定 是否垂直?若不存在,请说明理由.
是否垂直?若不存在,请说明理由. 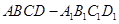 中,
中,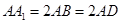 ,且
,且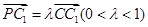 .
.
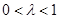 ,总有
,总有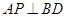 ;
;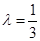 ,求二面角
,求二面角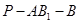 的余弦值;
的余弦值;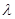 ,使得
,使得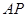 在平面
在平面 上的射影平分
上的射影平分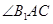 ?若存在, 求出
?若存在, 求出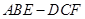 的三视图如图,
的三视图如图,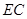 与
与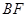 交于点
交于点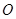 ,
,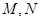 分别是直线
分别是直线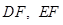 的中点,
的中点, 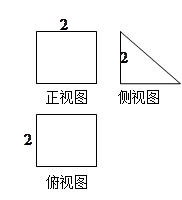
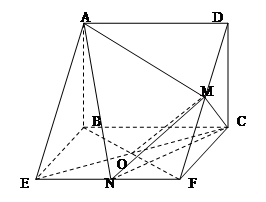
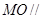 面
面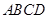 ;
;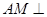 面
面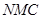 ;
;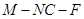 的平面角的余弦值.
的平面角的余弦值.
 ,
, ,E为棱
,E为棱 的中点.
的中点. ; (Ⅱ) 求证:
; (Ⅱ) 求证: 平面
平面 ;
; 的体积.
的体积.
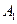 点,且
点,且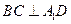 ;
;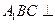 平面
平面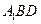 ;
;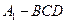 的体积.
的体积.