题目内容

11．若集合M={y|y=2x，x≤1}，N={x|$\frac{x-1}{x+1}$≤0}，则  N∩M（　　）
A．（1-1，]B．（0，1]C．[-1，1]D．（-1，2]

分析 求出M中y的范围确定出M，求出N中x的范围确定出N，找出M与N的交集即可．

解答 解：由M中y=2x，x≤1，得到0＜y≤2，即M=（0，2]，
由N中不等式变形得：（x-1）（x+1）≤0，且x+1≠0，
解得：-1＜x≤1，即N=（-1，1]，
则M∩N=（0，1]，
故选：B．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
1．将全体正整数排成如图的一个三角形数阵，按照此排列规律，第10行从左向右的第5个数为50．
2．为了保护环境，某市设立了若干个自行车自动租赁点，规定租车时间不超过一小时不收费，一小时以上不超过两小时收费一元，两小时以上，不超过三小时收费两元（不足一小时，按一小时计），甲、乙两人各租车一辆，甲、乙租车时间不超过一小时的概率为$\frac{1}{2}$、$\frac{1}{4}$，一小时以上，不超过两小时的概率为$\frac{1}{4}$、$\frac{1}{2}$，且两人租车时间都不会超过三小时（甲、乙两人租车时间相互独立）．
（1）求甲、乙两人所付租车费相等的概率；
（2）设两人租车费用之和为ξ，求ξ的分布列及数学期望．
19．已知向量$\overrightarrow{m}$=（$\sqrt{3}$，sinθ），$\overrightarrow{n}$=（1，cosθ），θ∈（0，$\frac{π}{2}$），$\overrightarrow{m}$与$\overrightarrow{n}$共线．
（Ⅰ）求θ的值；
（Ⅱ）求函数f（x）=sinx+sin（x-θ）在区间上[0，$\frac{5π}{6}$]的最大值和最小值．
6．已知函数f（x）满足：x≥4，则f（x）=2x；当x＜4时f（x）=f（x+1），则f（2+log${\;}_{\frac{1}{2}}$3）=$\frac{64}{3}$．
16．执行如图所示的程序框图，若a=1，b=2，则输出的结果是（　　）
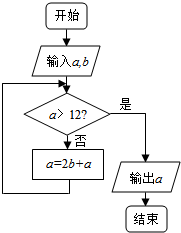
A．9B．11C．13D．15
3．在△ABC中，若角A为锐角，且$\overrightarrow{AB}$=（2，3），$\overrightarrow{AC}$=（3，m），则实数m的取值范围是$（-2，\frac{9}{2}）∪（\frac{9}{2}，+∞）$．
20．设直线l的参数方程为$\left\{\begin{array}{l}x=\frac{3}{2}+tsin\frac{5π}{6}\\ y=-tcos\frac{π}{6}\end{array}$（t为参数），若以直角坐标系xOy的O点为极点，Ox轴为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程为ρ=$\frac{6cosθ}{{{{sin}^2}θ}}$．
（Ⅰ）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
（Ⅱ）若直线l与曲线C交于A，B两点，求|AB|．
1．设函数f（x）=$\frac{a}{{x}^{2}}$+lnx，g（x）=x3-x2-3．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）如果对于任意的${x_1}，{x_2}∈[{\frac{1}{3}，2}]$，都有x1•f（x1）≥g（x2）成立，试求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网