题目内容
某中学高三文科班学生参加了数学与地理水平测试,学校从测试合格的学生中随机抽取100人的成绩进行统计分析.抽取的100人的数学与地理的水平测试成绩如下表:
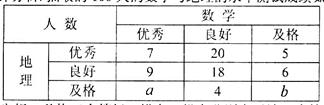
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(2)若样本中 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.

成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(2)若样本中
 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.(1)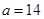 ,
,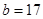 ; (2)
; (2) .
.
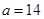 ,
,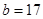 ; (2)
; (2) .
. 试题分析:(1)由
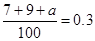 ,得
,得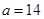 ,
, 根据
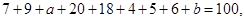 可得
可得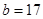 ;
;(2)由题意知
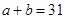 ,且
,且 ,
,满足条件的
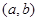 有
有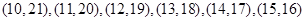 ,
,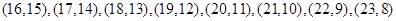 共14组.
共14组.且每组出现的可能性相同.
其中数学成绩优秀的人数比及格的人数少的有:
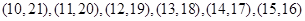 共6组.利用古典概型概率的计算公式即得.
共6组.利用古典概型概率的计算公式即得.(1)由
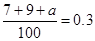 ,得
,得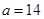 , 3分
, 3分∵
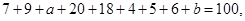 ∴
∴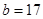 ,
,∴
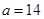 ,
,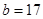 ; 6分
; 6分(2)由题意知
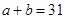 ,且
,且 ,
,∴满足条件的
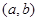 有
有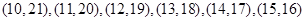 ,
,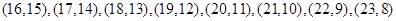 共14组.
共14组.且每组出现的可能性相同. 9分
其中数学成绩优秀的人数比及格的人数少的有:
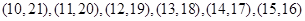 共6组. 11分
共6组. 11分∴数学成绩为优秀的人数比及格的人数少的概率为
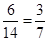 . 12分
. 12分
练习册系列答案
相关题目
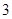 个小组的频率之比为
个小组的频率之比为 ,其中第
,其中第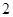 小组的频数为
小组的频数为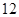 ,则报考飞行员的总人数是 .
,则报考飞行员的总人数是 .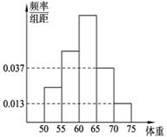
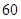 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过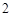 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过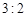 .
.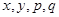 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).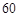 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定 人,若需从这
人,若需从这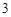 人进行问卷调查,设
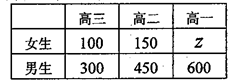
人进行问卷调查,设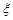 为选取的
为选取的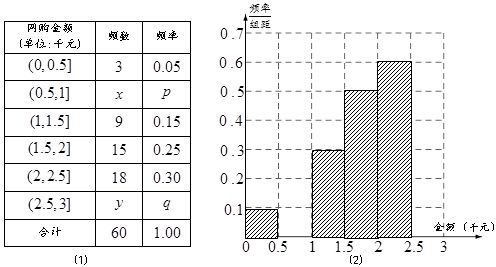
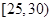 ,第2组
,第2组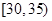 ,第3组
,第3组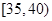 ,第4组
,第4组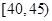 ,第5组
,第5组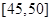 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。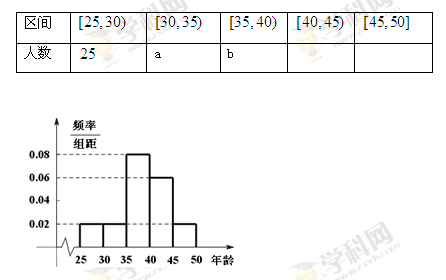
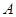 组
组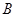 组
组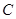 组
组
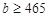 ,
,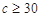 ,求通过测试的概率.
,求通过测试的概率.