题目内容
已知函数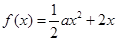 ,
,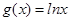 .
.
(1)如果函数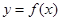 在
在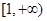 上是单调增函数,求
上是单调增函数,求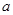 的取值范围;
的取值范围;
(2)是否存在实数 ,使得方程
,使得方程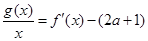 在区间
在区间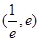 内有且只
内有且只
有两个不相等的实数根?若存在,请求出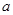 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】
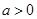 (
(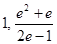 )
)
【解析】解:(1)当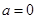 时,
时,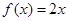 在
在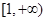 上是单调增函数,符合题意.………1分
上是单调增函数,符合题意.………1分
当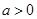 时,
时,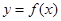 的对称轴方程为
的对称轴方程为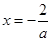 ,
,
由于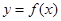 在
在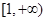 上是单调增函数,
上是单调增函数,
所以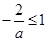 ,解得
,解得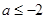 或
或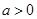 ,
,
所以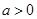 .
……………………3分
.
……………………3分
当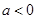 时,不符合题意.
时,不符合题意.
综上,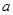 的取值范围是
的取值范围是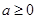 .
……………………4分
.
……………………4分
(2)把方程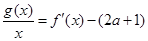 整理为
整理为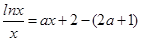 ,
,
即为方程 .
……………………5分
.
……………………5分
设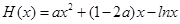
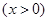 ,
,
原方程在区间(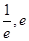 )内有且只有两个不相等的实数根, 即为函数
)内有且只有两个不相等的实数根, 即为函数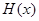 在区间(
在区间(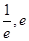 )内有且只有两个零点.
………………6分
)内有且只有两个零点.
………………6分
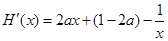
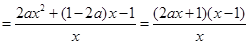 …………………7分
…………………7分
令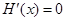 ,因为
,因为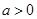 ,解得
,解得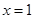 或
或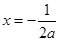 (舍) …………………8分
(舍) …………………8分
当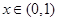 时,
时, 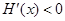 ,
, 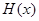 是减函数;
是减函数;
当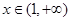 时,
时, 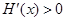 ,
,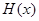 是增函数.
…………………10分
是增函数.
…………………10分
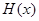 在(
在(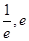 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需
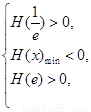 …………………13分
…………………13分
即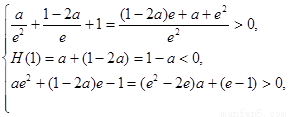 ∴
∴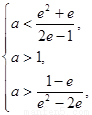
解得 , 所以
, 所以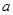 的取值范围是(
的取值范围是(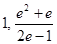 ) . ………………14分
) . ………………14分

练习册系列答案
相关题目