题目内容
如图:二面角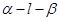 的大小是
的大小是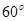 ,线段
,线段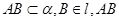 与
与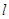 所成角为
所成角为 ,则
,则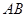 与平面
与平面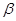 所成角的正弦值是_________ .
所成角的正弦值是_________ . 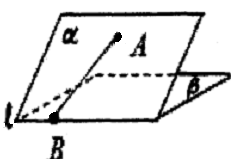
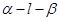 的大小是
的大小是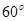 ,线段
,线段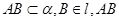 与
与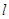 所成角为
所成角为 ,则
,则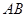 与平面
与平面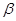 所成角的正弦值是_________ .
所成角的正弦值是_________ . 
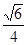
试题分析:过点A作平面β的垂线,垂足为C,
在β内过C作l的垂线.垂足为D
连接AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角α-l-β的平面角,为60°
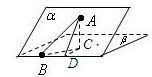
又由已知,∠ABD=45°
连接CB,则∠ABC为AB与平面β所成的角,设AD=2,则AC=
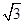 ,CD=1,AB=AD:sin450=2
,CD=1,AB=AD:sin450=2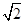 ,∴sin∠ABC=AC:AB=
,∴sin∠ABC=AC:AB=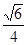 ;故答案为
;故答案为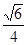 .
.点评:解决该试题的关键是过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D,连接AD,从而∠ADC为二面角α-l-β的平面角,连接CB,则∠ABC为AB与平面β所成的角,在直角三角形ABC中求出此角即可.

练习册系列答案
相关题目
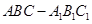 中,
中,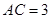 ,
,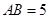 ,
, .
.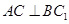 ;
;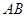 线段上存在一点
线段上存在一点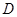 ,使得
,使得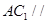 平面
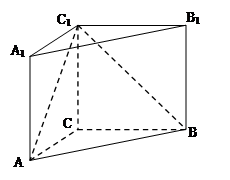
平面 ?
?
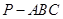 的棱
的棱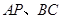 的中点,
的中点,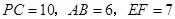 ,则异面直线AB与PC所成的角为( )
,则异面直线AB与PC所成的角为( )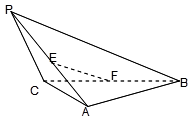
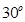
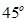
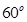
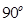
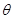 ,现沿对角线BD折成60°的二面角,翻折后
,现沿对角线BD折成60°的二面角,翻折后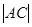 =
=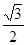 a,则锐角A是( )
a,则锐角A是( )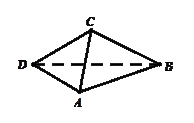
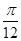
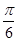
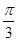
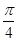
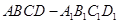 的底面边长为2,高为4,则异面直线
的底面边长为2,高为4,则异面直线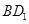 与AD所成角的余弦值是________.
与AD所成角的余弦值是________.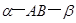 是直二面角,P为棱AB上一点,PQ、PR分别在平面
是直二面角,P为棱AB上一点,PQ、PR分别在平面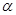 、
、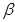 内,且
内,且 ,则
,则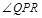 为( )
为( )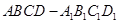 (底面是正方形,侧棱垂直底面的四棱柱)中,
(底面是正方形,侧棱垂直底面的四棱柱)中,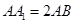 ,则异面直线
,则异面直线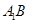 与
与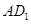 所成角的余弦值为( )
所成角的余弦值为( )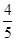
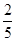
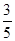
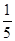
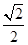 ,E为侧棱PC的中点,则PA与BE所成的角为( )
,E为侧棱PC的中点,则PA与BE所成的角为( )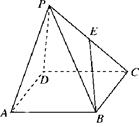
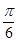
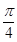
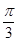

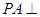 平面
平面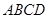 ,四边形
,四边形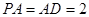 ,点
,点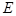 、
、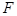 、
、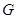 分别为线段
分别为线段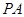 、
、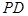 和
和 的中点.
的中点.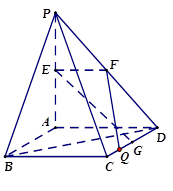
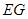 与
与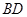 所成角的余弦值;
所成角的余弦值; ,使得点
,使得点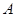 到平面
到平面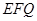 的距离恰为
的距离恰为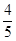 ?若存在,求出线段
?若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.