题目内容
(本题满分14分)本题共有3个小题,第1小题满分4分,第2、3小题满分各5分)
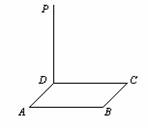
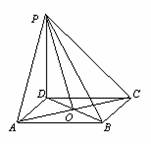
已知边长为6的正方形ABCD所在平面外一点P,PD^平面ABCD,PD=8,(1)连接PB、AC,证明:PB ^ AC;(2)连接PA,求PA与平面PBD所成的角的大小;(3)
|
(1)证明:连接BD,在正方形ABCD中,AC ^ BD,
又PD^平面ABCD,所以,PD^AC,………………………………………………2分
所以AC ^平面PBD,故PB ^ A C.…………………………………………………4分
|
在DAPO中,AO=3,AP = 10
所以 sin ÐAPO =
ÐAPO=arcsin…………………………8分
PA与平面PBD所成的角的大小为arcsin……………………………………9分
(3)解:连接PC,设点D到平面PAC的距离为h,……………………………10分
则有VD–PAC =VP–ACD,即:´ SDPAC ´ h =´PD´AD´DC………………………12分
在DPAC中,显然PO^AC,PO=
h =
所以点D到平面PAC的距离为……………………………………14分

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本) 年销售量.
年销售量. 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;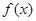 =
=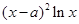 ,
,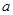 ∈R
∈R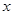 =
=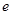 为
为 的极值点,求实数
的极值点,求实数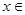 (0,3
(0,3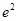 成立.
成立.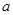 元,每期利率为
元,每期利率为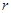 ,设存期为
,设存期为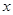 ,本利和(本金加上利息)为
,本利和(本金加上利息)为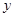 元。
元。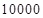 元,每期利率为
元,每期利率为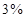 ,试计算
,试计算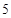 期后的本利和。
期后的本利和。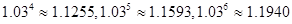 )
) 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
,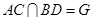 .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求证:
;(Ⅱ)求证: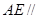 平面
平面 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥 的体积.
的体积.