题目内容
10.已知函数f(x)=$\frac{si{n}^{2}θ+3}{\sqrt{si{n}^{2}θ+2}}$,求它的最小值.分析 把已知的函数解析式变形,然后换元,再利用“对勾”函数的单调性求得答案.
解答 解:f(x)=$\frac{si{n}^{2}θ+3}{\sqrt{si{n}^{2}θ+2}}$=$\frac{si{n}^{2}θ+2+1}{\sqrt{si{n}^{2}θ+2}}$=$\sqrt{si{n}^{2}θ+2}+\frac{1}{\sqrt{si{n}^{2}θ+2}}$,
令$\sqrt{si{n}^{2}θ+2}=t$,则t∈[$\sqrt{2},\sqrt{3}$].
原函数化为g(t)=$t+\frac{1}{t}$,在[$\sqrt{2},\sqrt{3}$]上为增函数,
∴当t=$\sqrt{2}$时,$g(t)_{min}=\sqrt{2}+\frac{1}{\sqrt{2}}=\sqrt{2}+\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2}$.
∴f(x)=$\frac{si{n}^{2}θ+3}{\sqrt{si{n}^{2}θ+2}}$的最小值为$\frac{3\sqrt{2}}{2}$.
点评 本题考查三角函数最值的求法,训练了换元法,训练了利用“对勾”函数的单调性求函数的值域,是中档题.

练习册系列答案
相关题目
20.已知a、b表示两条不同的直线,α,β表示两个不同的平面,则下列命题正确的是( )
| A. | 若α∥β,a∥α,b∥β,则a∥b | B. | 若a?α,b?β,a∥b,则α∥β | ||
| C. | 若a⊥α,b⊥β,α⊥β,则a∥b | D. | 若a⊥α,b⊥β,a⊥b,则α⊥β |
18.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5},集合B={1,3,4,6,7},则集合A∩∁UB=( )
| A. | {3} | B. | {2,5} | C. | {2,3,5} | D. | {2,3,5,8} |
5.设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
| A. | f(x)g(x)是偶函数 | B. | |f(x)|g(x)是奇函数 | C. | f(-x)是奇函数 | D. | |g(x)|是奇函数 |
20.奇函数f(x)在(0,+∞)上满足:任意x1<x2,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,且f(2)=0,则不等式 $\frac{f(x)-f(-x)}{x}$<0的解集为( )
| A. | (-2,0)∪(0,2) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |
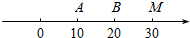 如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.