题目内容
11. 如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.(Ⅰ)求证:AC⊥平面BCE;
(Ⅱ)求三棱锥A-CDE的体积;
(Ⅲ)线段EF上是否存在一点M,使得BM⊥CE?若存在,确定M点的位置;若不存在,请说明理由.
分析 (I)如图所示,取AB的中点N,连接CN,可得四边形ADCN是正方形,可得NA=NB=NC,可得AC⊥CB,利用AF⊥平面ABCD,AF∥BE,可得BE⊥平面ABCD,即可证明.
(II)利用V三棱锥A-CDE=V三棱锥E-ACD=$\frac{1}{3}BE•{S}_{ACD}$即可得出.
(III)线段EF上存在一点M为线段EF的中点,使得BM⊥CE.连接MN,BM,EN,则四边形BEMN为正方形,可得BM⊥EN,利用线面面面垂直的判定与性质定理可得:
CN⊥平面ABEF,可得CN⊥BM,又BM⊥CE.即可证明BM⊥平面CEN.
解答 (I)证明:如图所示,取AB的中点N,连接CN,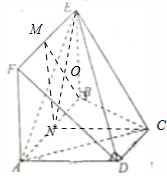
则四边形ADCN是正方形,可得NA=NB=NC,
∴AC⊥CB,
∵AF⊥平面ABCD,AF∥BE,
∴BE⊥平面ABCD,
∴BE⊥AC,
又BE∩BC=B,
∴AC⊥平面BCE.
(II)解:V三棱锥A-CDE=V三棱锥E-ACD=$\frac{1}{3}BE•{S}_{ACD}$=$\frac{1}{3}×2×\frac{1}{2}×{2}^{2}$=$\frac{4}{3}$.
(III)解:线段EF上存在一点M为线段EF的中点,使得BM⊥CE.
连接MN,BM,EN,则四边形BEMN为正方形,
∴BM⊥EN,
∵CN⊥AB,平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,
∴CN⊥平面ABEF,
∴CN⊥BM,
又CN∩EN=N,
∴BM⊥平面CEN,
∴BM⊥CE.
点评 本题考查了线面面面垂直的判定与性质定理、正方形的判定与性质定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.函数f(x)=$\left\{\begin{array}{l}{3,x≥m}\\{{x}^{2}+4x+2,x<m}\end{array}\right.$,函数g(x)=f(x)-x恰有三个零点,则实数m的取值范围为( )
| A. | [-2,3] | B. | [-1,3] | C. | (-2,3] | D. | (-1,3] |
20.在棱长为3的正方体ABCD-A1B1C1D1中,P在线段BD1上,且$\frac{BP}{P{D}_{1}}=\frac{1}{2}$,M为线段B1C1上的动点,则三棱锥M-PBC的体积为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{9}{2}$ | D. | 与M点的位置有关 |