题目内容
【题目】定义:设![]() 是正整数,如果对任意正整数
是正整数,如果对任意正整数![]() ,当
,当![]() 时,即有
时,即有![]() ,那么称数列
,那么称数列![]() 的前
的前![]() 项可被数列
项可被数列![]() 的第
的第![]() 项替换.已知数列
项替换.已知数列![]() 的前
的前![]() 项和是
项和是![]() ,数列
,数列![]() 是公比为1的等差数列.
是公比为1的等差数列.
(1)求数列![]() 的通项公式(用
的通项公式(用![]() ,
,![]() 表示);
表示);
(2)已知![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ;
;
①求证:数列![]() 为等比数列,并求
为等比数列,并求![]() 的通项公式;
的通项公式;
②若数列![]() 的前
的前![]() 可被数列
可被数列![]() 的前
的前![]() 项替换,且
项替换,且![]() 的最大值为8,求
的最大值为8,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①证明见解析,
;(2)①证明见解析,![]() ,②
,②![]()
【解析】
(1)依题意可得![]() ,再利用
,再利用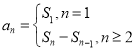 计算可得;
计算可得;
(2)①由![]() ,得到
,得到![]() ,即可得证,还需计算
,即可得证,还需计算![]() ;
;
②由题意知![]() 对一切
对一切![]() 恒成立,即
恒成立,即![]() ,令
,令![]() ,判断
,判断![]() 的单调性,即可得到
的单调性,即可得到![]() 的取值范围.
的取值范围.
(1)∵![]() 是公差为1的等差数列且首项为
是公差为1的等差数列且首项为![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() 也满足上式,
也满足上式,
∴![]() .
.
(2)①∵![]() ①
①
当![]() 时,
时,![]() ②
②
①-②得![]() ,
,![]()
在①式令![]() ,得
,得![]() ,
,
∴![]() ,
,
故![]() ,
,
∴![]() 为等比数列,
为等比数列,![]() .
.
②由题意知![]() 对一切
对一切![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() ,
,
令![]() ,
,
![]() ,
,
∴![]() 单调递增,
单调递增,
∴![]() .
.
另一方面![]() 对一切
对一切![]() 且
且![]() 恒成立,
恒成立,
即![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】某机构对某市工薪阶层的收入情况与超前消费行为进行调查,随机抽查了200人,将他们的月收入(单位:百元)频数分布及超前消费的认同人数整理得到如下表格:
月收入(百元) |
|
|
|
|
|
|
频数 | 20 | 40 | 60 | 40 | 20 | 20 |
认同超前消费的人数 | 8 | 16 | 28 | 21 | 13 | 16 |
(1)根据以上统计数据填写下面![]() 列联表,并回答是否有99%的把握认为当月收入以8000元为分界点时,该市的工薪阶层对“超前消费”的态度有差异;
列联表,并回答是否有99%的把握认为当月收入以8000元为分界点时,该市的工薪阶层对“超前消费”的态度有差异;
月收入不低于8000元 | 月收入低于8000元 | 总计 | |
认同 | |||
不认同 | |||
总计 |
(2)若从月收入在![]() 的被调查对象中随机选取2人进行调查,求至少有1个人不认同“超前消费”的概率.
的被调查对象中随机选取2人进行调查,求至少有1个人不认同“超前消费”的概率.
参考公式: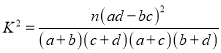 (其中
(其中![]() ).
).
附表:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】若养殖场每个月生猪的死亡率不超过![]() ,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只3 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
(1)从该养殖场2019年2月到6月这5个月中任意选取3个月,求恰好有2个月考核获得合格的概率;
(2)根据1月到8月的数据,求出月利润y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.001).
(3)预计在今后的养殖中,月利润与月养殖量仍然服从(2)中的关系,若9月份的养殖量为1.5万只,试估计:该月利润约为多少万元?
附:线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下: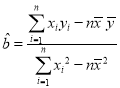 ,
,![]()
参考数据:![]() .
.