题目内容
(1)利用“五点法”画出函数f(x)=sin| 1 | 2 |
(2)求函数f(x)的单调减区间
分析:(1)分别令
x的值取0,
,π,
,2π,求出对应的x及f(x)值,然后利用“五点法”描出正弦型函数在一个周期上的五个关键点,进而即可得到函数f(x)=sin
x在长度为一个周期的闭区间的简图
(2)根据函数的图象,我们易分析出一个周期上函数的单调递减区间,加上周期后,即可得到函数f(x)的单调减区间.
| 1 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
(2)根据函数的图象,我们易分析出一个周期上函数的单调递减区间,加上周期后,即可得到函数f(x)的单调减区间.
解答:解:(1)令
x的值取0,
,π,
,2π,列表得:
函数f(x)=sin
x在长度为一个周期的闭区间的简图如下图所示:
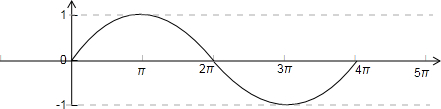
(2)由图可知在[π,3π]上函数为减函数,
又∵函数f(x)=sin
x的周期为4π,
∴则函数的单调区间为[π+4kπ,3π+4kπ],(k∈Z)
| 1 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
|
0 |
|
π |
|
2π | ||||||
| x | 0 | π | 2π | 3π | 4π | ||||||
f(x)=sin
|
0 | 1 | 0 | -1 | 0 |
| 1 |
| 2 |

(2)由图可知在[π,3π]上函数为减函数,
又∵函数f(x)=sin
| 1 |
| 2 |
∴则函数的单调区间为[π+4kπ,3π+4kπ],(k∈Z)
点评:本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象正弦函数的单调性,其中利用五点法作出函数f(x)=sin
x的图象,是解答本题的关键.
| 1 |
| 2 |

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目