题目内容
设a>0,b>0,2c>a+b,求证:
(1)c2>ab;
(2)c- <a<c+
<a<c+ .
.
(1)c2>ab;
(2)c-
 <a<c+
<a<c+ .
.见解析
(1)∵a>0,b>0,∴2c>a+b≥2 ∴c>
∴c> >0,∴c2>ab.
>0,∴c2>ab.
(2)要证c- <a<c+
<a<c+
只要证- <a-c<
<a-c<
即证|a-c|< ,也就是(a-c)2<c2-ab
,也就是(a-c)2<c2-ab
而(a-c)2-(c2-ab)=a(a+b-2c)<0∴原不等式成立.
 ∴c>
∴c> >0,∴c2>ab.
>0,∴c2>ab.(2)要证c-
 <a<c+
<a<c+
只要证-
 <a-c<
<a-c<
即证|a-c|<
 ,也就是(a-c)2<c2-ab
,也就是(a-c)2<c2-ab而(a-c)2-(c2-ab)=a(a+b-2c)<0∴原不等式成立.

练习册系列答案
相关题目
 ,
, ,
, ,求证:
,求证: ,
, ,
, .
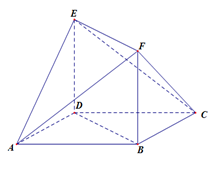
. 是菱形,
是菱形, 是矩形,
是矩形, 平面
平面 ,
, .
.
 平面
平面 ;
; 为直二面角,求直线
为直二面角,求直线 与平面
与平面 所成的角
所成的角 的正弦值.
的正弦值. -2
-2 与
与 -
-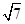 的大小关系是______________.
的大小关系是______________.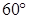 ”时,反设正确的是
”时,反设正确的是
 ,函数
,函数 单调递减,
单调递减, 上为增函数,若“
上为增函数,若“ ”为假,“
”为假,“ ”为真,求实数
”为真,求实数 的取值范围。
的取值范围。 求证:
求证: