题目内容
二次函数y=f(x)满足:①f(0)=1;②f(x+1)-f(x)=2x.
(1)求f(x)的解析式;
(2)求f(x)在区间[-1,1]上的最大值和最小值;
(3)设g(x)=f(x-a),求g(x)在区间[-1,1]上的最大值.
(1)求f(x)的解析式;
(2)求f(x)在区间[-1,1]上的最大值和最小值;
(3)设g(x)=f(x-a),求g(x)在区间[-1,1]上的最大值.
分析:(1)设f(x)=y=ax2+bx+c(a≠0),由f(0)=1可求c,再由f(x+1)-f(x)=2x可求a,b的值,进而可求函数f(x)
(2)由f(x)=(x-
)2+
,x∈[-1,1],结合二次函数的图象可求函数的最值
(3)由g(x)=f(x-a)=x2-(2a+1)x+a2+a+1,x∈[-1,1],对称轴为:x=a+
,故需要考虑对称轴与区间[-1,1]的位置关系,从而可讨论①当a+
≥0;②当a+
<0时分别进行求解
(2)由f(x)=(x-
| 1 |
| 2 |
| 3 |
| 4 |
(3)由g(x)=f(x-a)=x2-(2a+1)x+a2+a+1,x∈[-1,1],对称轴为:x=a+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设f(x)=y=ax2+bx+c(a≠0)(1分)
由f(0)=1得,c=1(2分)
因为f(x+1)-f(x)=2x
所以a(x+1)2+b(x+1)-ax2-bx=2x,
即2ax+a+b=2x(4分)
所以
⇒
所以f(x)=x2-x+1(16分)
(2)∵f(x)=(x-
)2+
,x∈[-1,1]
当x=
时,ymin=
,(8分)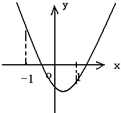
当x=-1时,ymax=3.(10分)
(3)∵g(x)=f(x-a)=x2-(2a+1)x+a2+a+1,x∈[-1,1]
对称轴为:x=a+
①当a+
≥0时,即:a≥-
;如图:
g(x)max=g(-1)=a2+3a+3(13分)
②当a+
<0时,即:a<-
;如图: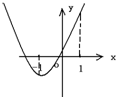
g(x)max=g(1)=a2-a+1(15分)
综上所述:g(x)max=
(16分)
(注:分四种情况讨论的每种(1分),总结论2分)
由f(0)=1得,c=1(2分)
因为f(x+1)-f(x)=2x
所以a(x+1)2+b(x+1)-ax2-bx=2x,
即2ax+a+b=2x(4分)
所以
|
|
所以f(x)=x2-x+1(16分)
(2)∵f(x)=(x-
| 1 |
| 2 |
| 3 |
| 4 |
当x=
| 1 |
| 2 |
| 3 |
| 4 |

当x=-1时,ymax=3.(10分)
(3)∵g(x)=f(x-a)=x2-(2a+1)x+a2+a+1,x∈[-1,1]
对称轴为:x=a+
| 1 |
| 2 |
①当a+
| 1 |
| 2 |
| 1 |
| 2 |
g(x)max=g(-1)=a2+3a+3(13分)
②当a+
| 1 |
| 2 |
| 1 |
| 2 |

g(x)max=g(1)=a2-a+1(15分)
综上所述:g(x)max=
|
|
(注:分四种情况讨论的每种(1分),总结论2分)
点评:本题主要考查了由二次函数的性质求解二次函数的解析式及二次函数在闭区间上的最值的求解,要注意分类讨论思想在解题中的应用,而讨论的根本思想在于判断二次函数的对称轴与所给区间的位置关系.

练习册系列答案
相关题目
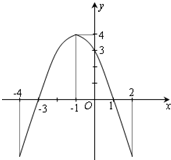 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象. 已知二次函数y=f(x)的图象如图所示.
已知二次函数y=f(x)的图象如图所示.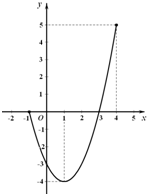 二次函数y=f(x)的图象的一部分如图所示.
二次函数y=f(x)的图象的一部分如图所示.