题目内容
 桑基鱼塘是广东省珠江三角洲一种独具地方特色的农业生产形式.
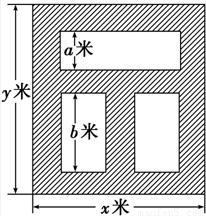
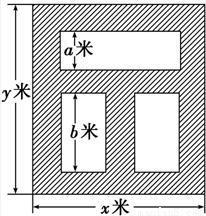
桑基鱼塘是广东省珠江三角洲一种独具地方特色的农业生产形式.某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块占地
1800平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土
堆在池塘四周形成基围(阴影部分所示)种植桑树,鱼塘周围的基围
宽均为2米,如图所示,池塘所占面积为S平方米,其中a:b=1:2.
(1)试用x,y表示S;
(2)若要使S最大,则x,y的值各为多少?
分析:(1)由已知该项目占地为1800平方米的矩形地块,我们可得xy=1800,结合图形还易得b=2a,及y=a+b+6=3a+6,由此我们易将池塘所占面积S表示为变量x,y的函数.
(2)要求S的最大值,我们有三种思路:①根据xy=1800,直接使用基本不等式;②根据xy=1800,消元后再使用基本不等式;③根据xy=1800,消元后利用导数判断函数的单调性,再求最大值.
(2)要求S的最大值,我们有三种思路:①根据xy=1800,直接使用基本不等式;②根据xy=1800,消元后再使用基本不等式;③根据xy=1800,消元后利用导数判断函数的单调性,再求最大值.
解答:解:(1)由题可得:xy=1800,b=2a,
则y=a+b+6=3a+6,
即a=
.
S=(x-4)a+(x-6)×b=(3x-16)
=1832-6x-
y(x>0).
(2)法一:S=1832-6x-
y≤1832-2
=1832-480=1352,
当且仅当6x=
y,即x=40,y=45时,S取得最大值1352.
法二:S=1800-6x-
×
+32=1832-(6x+
)≤1832-2
=1832-480=1352,
当且仅当6x=
,即x=40时取等号,S取得最大值.
此时y=
=45.
法三:设S=f(x)=1832-(6x+
)(x>0)
f′(x)=
-6=
.
令f′(x)=0,得x=40.
当0<x<40时,f′(x)>0;当x>40时,f′(x)<0.
∴当x=40时,S取得最大值,此时y=45.
则y=a+b+6=3a+6,
即a=
| y-6 |
| 3 |
S=(x-4)a+(x-6)×b=(3x-16)
| y-6 |
| 3 |
=1832-6x-
| 16 |
| 3 |
(2)法一:S=1832-6x-
| 16 |
| 3 |
6x×
|
=1832-480=1352,
当且仅当6x=
| 16 |
| 3 |
法二:S=1800-6x-
| 16 |
| 3 |
| 1800 |
| x |
| 9600 |
| x |
6x
|
=1832-480=1352,
当且仅当6x=
| 9600 |
| x |
此时y=
| 1800 |
| x |
法三:设S=f(x)=1832-(6x+
| 9600 |
| x |
f′(x)=
| 9600 |
| x2 |
| 6(40-x)(40+x) |
| x2 |
令f′(x)=0,得x=40.
当0<x<40时,f′(x)>0;当x>40时,f′(x)<0.
∴当x=40时,S取得最大值,此时y=45.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
相关题目
 (1) 试用
(1) 试用