题目内容
已知两点M(0,1)N(0,-1),平面上动点P(x,y)满足 .
.(Ⅰ)求动点P(x,y)的轨迹C的方程;
(Ⅱ)设Q(0,m),R(0,-m)(m≠0)是y轴上两点,过Q作直线与曲线C交于A、B两点,试证:直线RA、RB与y轴所成的锐角相等;
(Ⅲ).在Ⅱ的条件中,若m<0,直线AB的斜率为1,求△RAB面积的最大值.
【答案】分析:(1)先根足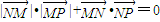 .把M,N和p的坐标代入整理得x2=4y,进而可得P点的轨迹方程.
.把M,N和p的坐标代入整理得x2=4y,进而可得P点的轨迹方程.
(2)设直线l的方程,与抛物线方程联立消去y,设A(x1,y1),B(x2,y2),根据韦达定理可得x1+x2和x1x2,要证明直线RA、RB与y轴所成的锐角相等,只要证明kRA+kRB=0,进而表示出两直线斜率,相加正好得0.
(3)根据斜率为1可得直线AB的方程,与抛物线方程联立消去y,根据判别式大于0求得m的范围,根据x1+x2和x1x2,表示出|AB|.记点R到AB的距离为d,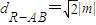 ,进而表示出△RAB面积,判别出关于m的函数的单调性,进而可求得△RAB面积的最大值.
,进而表示出△RAB面积,判别出关于m的函数的单调性,进而可求得△RAB面积的最大值.
解答:解:(Ⅰ)∵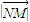
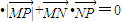 ,
,
∴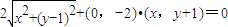
化简整理得x2=4y∴动点P(x,y)的轨迹C为抛物线,其方程为:x2=4y;
(Ⅱ)∵过Q作直线l与抛物线C交于A、B两点,∴l的斜率k存在
设直线l:y=kx+m与x2=4y联立,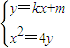
消去y得x2-4kx-4m=0,
则此方程有两个不相等的实数根,
∴△=16k2+16m>0,*
设A(x1,y1),B(x2,y2),
则x1+x2=4k,x1x2-4m,
要证直线RA、RB与y轴所成的锐角相等,
只要证明kRA+kRB=0
∵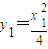 ,
,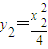
∴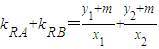
=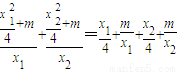
=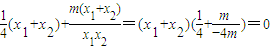 ,
,
∴命题成立.
Ⅲ.若直线AB的斜率k=1,
∴直线x-y+m=0,由Ⅱ.知消去y得x2-4x-4m=0,
由*式△>0得m>-1,∴-1<m<0,
且x1+x2=4,x1x2-4m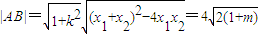 ,
,
记点R到AB的距离为d, ,
,
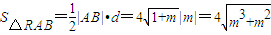 ,
,
设f(m)=m3+m2f′(m)=3m2+2m令f′(x)>0知f(m)
在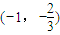 递增,在
递增,在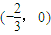 递减,
递减,
∴当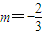 时f(m)有最大值,故S△RAB最大值为
时f(m)有最大值,故S△RAB最大值为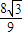 .
.
点评:本题主要考查了抛物线的标准方程和直线与抛物线的关系.直线与圆锥曲线的位置关系是历年高考命题的热点.在近几年的高考中,每年风格都在变换,考查思维的敏捷性,在探索中求创新.
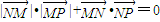 .把M,N和p的坐标代入整理得x2=4y,进而可得P点的轨迹方程.
.把M,N和p的坐标代入整理得x2=4y,进而可得P点的轨迹方程.(2)设直线l的方程,与抛物线方程联立消去y,设A(x1,y1),B(x2,y2),根据韦达定理可得x1+x2和x1x2,要证明直线RA、RB与y轴所成的锐角相等,只要证明kRA+kRB=0,进而表示出两直线斜率,相加正好得0.
(3)根据斜率为1可得直线AB的方程,与抛物线方程联立消去y,根据判别式大于0求得m的范围,根据x1+x2和x1x2,表示出|AB|.记点R到AB的距离为d,
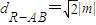 ,进而表示出△RAB面积,判别出关于m的函数的单调性,进而可求得△RAB面积的最大值.
,进而表示出△RAB面积,判别出关于m的函数的单调性,进而可求得△RAB面积的最大值.解答:解:(Ⅰ)∵
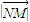
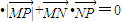 ,
,∴
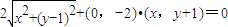
化简整理得x2=4y∴动点P(x,y)的轨迹C为抛物线,其方程为:x2=4y;
(Ⅱ)∵过Q作直线l与抛物线C交于A、B两点,∴l的斜率k存在
设直线l:y=kx+m与x2=4y联立,
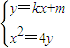
消去y得x2-4kx-4m=0,
则此方程有两个不相等的实数根,
∴△=16k2+16m>0,*
设A(x1,y1),B(x2,y2),
则x1+x2=4k,x1x2-4m,
要证直线RA、RB与y轴所成的锐角相等,
只要证明kRA+kRB=0
∵
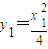 ,
,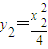
∴
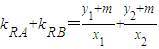
=
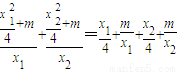
=
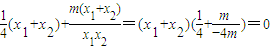 ,
,∴命题成立.
Ⅲ.若直线AB的斜率k=1,
∴直线x-y+m=0,由Ⅱ.知消去y得x2-4x-4m=0,
由*式△>0得m>-1,∴-1<m<0,
且x1+x2=4,x1x2-4m
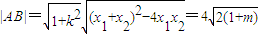 ,
,记点R到AB的距离为d,
 ,
,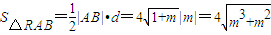 ,
,设f(m)=m3+m2f′(m)=3m2+2m令f′(x)>0知f(m)
在
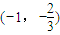 递增,在
递增,在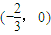 递减,
递减,∴当
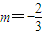 时f(m)有最大值,故S△RAB最大值为
时f(m)有最大值,故S△RAB最大值为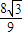 .
.点评:本题主要考查了抛物线的标准方程和直线与抛物线的关系.直线与圆锥曲线的位置关系是历年高考命题的热点.在近几年的高考中,每年风格都在变换,考查思维的敏捷性,在探索中求创新.

练习册系列答案
相关题目
 在平面直角坐标系中,点P(x,y)满足约束条件:
在平面直角坐标系中,点P(x,y)满足约束条件: