题目内容
 在平面直角坐标系中,点P(x,y)满足约束条件:
在平面直角坐标系中,点P(x,y)满足约束条件:
|
(1)在给定的坐标系中画出满足约束条件的可行域 (用阴影表示,并注明边界的交点);
(2)设u=
| y+7 |
| x+4 |
(3)已知两点M(2,1),O(0,0),求
| OM |
| OP |
分析:(1)先根据直线定出区域的边界,不等式确定区域,由约束条件画出可行域;
(2)u=
,利用u的几何意义求最值,只需求出何时可行域内的点与点(-4,-7)连线的斜率的最值,从而得到 u的取值范围.
(3)先根据向量的数量积公式得出
•
=2x+y,设z=2x+y,再利用z的几何意义求最值,只需求出直线z=2x+y经过点A时,z取到最大值,从而得到答案即可.
(2)u=
| y+7 |
| x+4 |
(3)先根据向量的数量积公式得出
| OM |
| OP |
解答:解:(1)由
得
,∴A(4,1)…(1分)
由
得
,∴B(-1,-6)…(2分)
由
得
,∴C(-3,2)…(3分)
画出可行域N,如右下图所示…(4分)
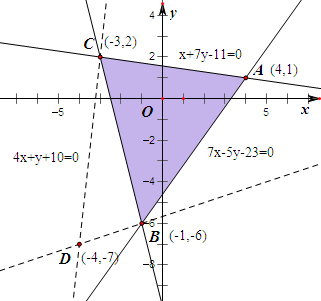
(2)u=
=kDP.…(5分)
当直线DP与直线DB重合时,倾斜角最小且为锐角,此时kDB=
; …(6分)
当直线DP与直线DC重合时,倾斜角最大且为锐角,此时kDC=9; …..(7分)
所以u=
的取值范围为[
,9].…(8分)
(3)
•
=(2,1)•(x,y)=2x+y,…..(10分)
设z=2x+y,则y=-2x+z,…..…(11分)z表示直线y=-2x+z在y轴上的截距,…(12分)
当直线y=-2x+z经过点A时,z取到最大值,…(13分)
这时z的最大值为zmax=2×4+1=9.….(14分)
|
|
由
|
|
由
|
|
画出可行域N,如右下图所示…(4分)

(2)u=
| y-(-7) |
| x-(-4) |
当直线DP与直线DB重合时,倾斜角最小且为锐角,此时kDB=
| 1 |
| 3 |
当直线DP与直线DC重合时,倾斜角最大且为锐角,此时kDC=9; …..(7分)
所以u=
| y+7 |
| x+4 |
| 1 |
| 3 |
(3)
| OM |
| OP |
设z=2x+y,则y=-2x+z,…..…(11分)z表示直线y=-2x+z在y轴上的截距,…(12分)
当直线y=-2x+z经过点A时,z取到最大值,…(13分)
这时z的最大值为zmax=2×4+1=9.….(14分)
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目