题目内容
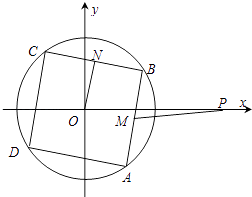
【题目】设P为双曲线 ![]() =1右支上的任意一点,O为坐标原点,过点P作双曲线两渐近线的平行线,分别与两渐近线交于A,B两点,则平行四边形PAOB的面积为 .
=1右支上的任意一点,O为坐标原点,过点P作双曲线两渐近线的平行线,分别与两渐近线交于A,B两点,则平行四边形PAOB的面积为 .
【答案】15
【解析】解:方法一:双曲线 ![]() =1的渐近线方程为y=±
=1的渐近线方程为y=± ![]() x, 不妨设P为双曲线右支上一点,其坐标为P(6secφ,5tanφ),
x, 不妨设P为双曲线右支上一点,其坐标为P(6secφ,5tanφ),
则直线PA的方程为y﹣5tanφ=﹣ ![]() (x﹣6secφ),
(x﹣6secφ),
将y= ![]() x代入,解得点A的横坐标为xA=3(secφ+tanφ).
x代入,解得点A的横坐标为xA=3(secφ+tanφ).
同理可得,点B的横坐标为xB=3(secφ﹣tanφ).
设∠AOF=α,则tanα= ![]() .
.
∴平行四边形PAOB的面积为S□PAOB=|OA||OB|sin2α= ![]()
![]() sin2α=
sin2α= ![]() sin2α=
sin2α= ![]() tanα=18×
tanα=18× ![]() =15,
=15,
平行四边形PAOB的面积15,
方法二:双曲线 ![]() =1的渐近线方程为y=±
=1的渐近线方程为y=± ![]() x,P(x0 , y0)直线PA的方程为y﹣y0=﹣
x,P(x0 , y0)直线PA的方程为y﹣y0=﹣ ![]() (x﹣x0),
(x﹣x0),
直线OB的方程为y= ![]() x,
x,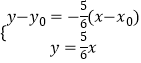 ,解得xA=
,解得xA= ![]() (6y0+5x0).又P到渐近线OA的距离d=
(6y0+5x0).又P到渐近线OA的距离d= ![]() =
= ![]() ,又tan∠xOA=
,又tan∠xOA= ![]() ∴cos∠xOA=
∴cos∠xOA= ![]() ,
,
∴平行四边形OQPR的面积S=2S△OPA=|OA|d= ![]() =
= ![]() ×
× ![]() 丨6y0+5x0丨×
丨6y0+5x0丨× ![]() = ×
= × ![]() 900=15,
900=15,
所以答案是:15.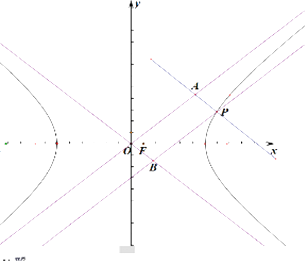

【题目】2016年下半年,锦阳市教体局举行了市教育系统直属单位职工篮球比赛,以增强直属单位间的交流与合作,组织方统计了来自A1 , A2 , A3 , A4 , A5等5个直属单位的男子篮球队的平均身高与本次比赛的平均得分,如表所示:
单位 | A1 | A2 | A3 | A4 | A5 |
平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
平均得分y | 62 | 64 | 66 | 70 | 68 |
注:回归当初 ![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为  ,
, ![]() .
.
(1)根据表中数据,求y关于x的线性回归方程;(系数精确到0.01)
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)