题目内容
在椭圆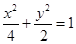 中,
中,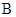 为椭圆上的一点,过坐标原点的直线交椭圆于
为椭圆上的一点,过坐标原点的直线交椭圆于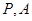 两点,其中
两点,其中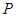 在第一象限,过
在第一象限,过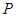 作
作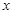 轴的垂线,垂足为
轴的垂线,垂足为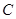 ,连接
,连接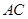 ,
,
(1)若直线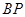 与
与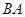 的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
(2)若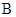 为
为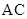 的延长线与椭圆的交点,求证:
的延长线与椭圆的交点,求证: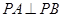 .
.
【答案】
解:(1)
设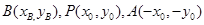
则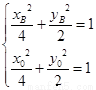 两式相减得,
两式相减得,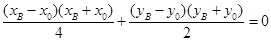
而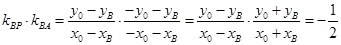 ……4分
……4分
(2)设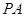 的方程为
的方程为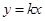 代入
代入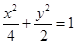 ,解得
,解得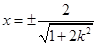 .
.
记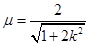 ,则
,则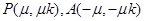 ,于是
,于是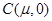 .
.
故直线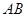 的斜率为
的斜率为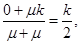 其方程为
其方程为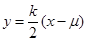
代入椭圆方程得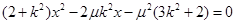 ,
,
解得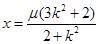 或
或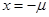 ,因此得
,因此得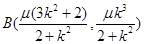 ,
,
于是直线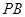 的斜率为
的斜率为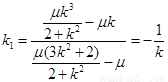 ,因此
,因此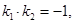
所以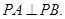 ……10分.
……10分.
【解析】略

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
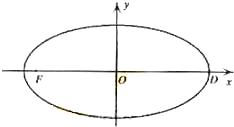 已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为
已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为
 (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被 为曲线
为曲线 在圆
在圆 上,
上, ,曲线
,曲线
 ,直线
,直线 , ………………3分
, ………………3分  ,可得
,可得 
 ,∴
,∴
 ,
,  ,则
,则 ,
,  得到。
得到。 ,
, ,
, , ………………10分
, ………………10分 ,
, ,
,  ,即只要
,即只要 ………………12分
………………12分  时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 ,使得
,使得 总能被
总能被 轴平分
轴平分