题目内容
(本题满分12分)已知函数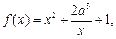 其中
其中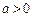 .
.
(I)若曲线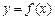 在
在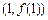 处的切线与直线
处的切线与直线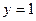 平行,求
平行,求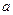 的值;
的值;
(II)求函数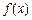 在区间
在区间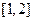 上的最小值
上的最小值
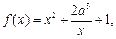 其中
其中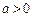 .
.(I)若曲线
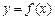 在
在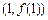 处的切线与直线
处的切线与直线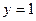 平行,求
平行,求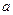 的值;
的值;(II)求函数
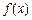 在区间
在区间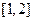 上的最小值
上的最小值解: ................2分
................2分
(I)由题意可得
 ,解得
,解得 ,....3分
,....3分
此时 ,在点
,在点 处的切线为
处的切线为 ,与直线
,与直线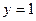 平行.故所求
平行.故所求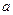 值为1........4分
值为1........4分
(II)由 可得
可得 ,,...... 5分
,,...... 5分
① 当 时,
时, 在
在 上恒成立 所以
上恒成立 所以 在
在 上递增,
上递增,
② 所以 在
在 上的最小值为
上的最小值为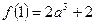 ........6分
........6分
②当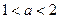 时,
时,
由上表可得 在
在 上的最小值为
上的最小值为 ...........8分
...........8分
③当 时,
时, 在
在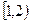 上恒成立,所以
上恒成立,所以 在
在 上递减 ..........9分
上递减 ..........9分
所以 在
在 上的最小值为
上的最小值为  . ........10分
. ........10分
综上讨论,可知:当 时,
时, 在
在 上的最小值为
上的最小值为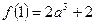 ;
;
当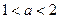 时,
时, 在
在 上的最小值为
上的最小值为 ;当
;当 时,
时, 在
在 上的最小值为
上的最小值为 . ........12分
. ........12分
 ................2分
................2分(I)由题意可得

 ,解得
,解得 ,....3分
,....3分此时
 ,在点
,在点 处的切线为
处的切线为 ,与直线
,与直线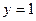 平行.故所求
平行.故所求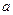 值为1........4分
值为1........4分(II)由
 可得
可得 ,,...... 5分
,,...... 5分① 当
 时,
时, 在
在 上恒成立 所以
上恒成立 所以 在
在 上递增,
上递增,② 所以
 在
在 上的最小值为
上的最小值为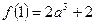 ........6分
........6分②当
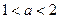 时,
时, |  |  |  |
 | - | 0 | + |
 |  | 极小 |  |
 在
在 上的最小值为
上的最小值为 ...........8分
...........8分③当
 时,
时, 在
在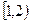 上恒成立,所以
上恒成立,所以 在
在 上递减 ..........9分
上递减 ..........9分所以
 在
在 上的最小值为
上的最小值为  . ........10分
. ........10分综上讨论,可知:当
 时,
时, 在
在 上的最小值为
上的最小值为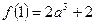 ;
;当
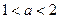 时,
时, 在
在 上的最小值为
上的最小值为 ;当
;当 时,
时, 在
在 上的最小值为
上的最小值为 . ........12分
. ........12分略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
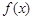 是奇函数,且当
是奇函数,且当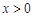 时,
时,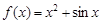 ,则当
,则当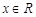 时,
时,

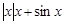

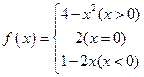 ,
,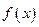 图像;
图像;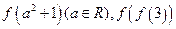 的值;
的值;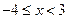 时,求
时,求 所过定点的横、纵坐标分别是等差数列
所过定点的横、纵坐标分别是等差数列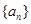 的第二项与第三项,若
的第二项与第三项,若 ,数列
,数列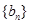 的前
的前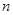 项和为
项和为 ,则
,则 =( )
=( )


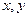 (单位为:
(单位为: )的矩形,上部是等腰直角三角形,要求框架围成的总面积为
)的矩形,上部是等腰直角三角形,要求框架围成的总面积为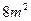 ,问:
,问: )时用料最省?
)时用料最省?


 ,
, 。
。 ;
; 的解集;
的解集; 时,求函数
时,求函数 的最大值。
的最大值。 ,则r = .
,则r = . 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,对于任意
,对于任意 ,都有
,都有 恒成立,则
恒成立,则 的值为 。
的值为 。