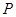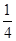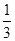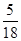��Ŀ����
����С������12�֣�ij�̳�Ϊ�����˿������Ƴ�һ���Żݻ.��������£����Ѷ�ÿ��100Ԫ��ת����ͼ��ʾ���� ΪԲ�ĵ�ת��һ�Σ��������Ӧ���ķ�ȯ���ٶ�ָ��ȿ��ܵ�ָ����һλ�ã���ָ�������ı߽磩. ��ָ��ͣ��A����ȯ60Ԫ��ͣ��B����ȯ30Ԫ��ͣ��C����ȯ. ���磺����218Ԫ����ת��ת��2�Σ�����õķ�ȯ��������ν��֮��.
ΪԲ�ĵ�ת��һ�Σ��������Ӧ���ķ�ȯ���ٶ�ָ��ȿ��ܵ�ָ����һλ�ã���ָ�������ı߽磩. ��ָ��ͣ��A����ȯ60Ԫ��ͣ��B����ȯ30Ԫ��ͣ��C����ȯ. ���磺����218Ԫ����ת��ת��2�Σ�����õķ�ȯ��������ν��֮��.
������ijλ�˿�����128Ԫ����ȯ������30Ԫ�ĸ��ʣ�
������ijλ�˿�ǡ������280Ԫ��������������˻������÷�ȯ�Ľ���Ϊ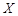 ��Ԫ��.���������
��Ԫ��.���������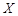 �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
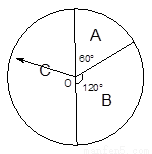
(��) ������128Ԫ�Ĺ˿ͣ���ȯ������30Ԫ�ĸ�����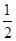 .
.
�����������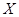 �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
0 |
30 |
60 |
90 |
120 |
|
|
|
|
|
|
|
����ѧ����
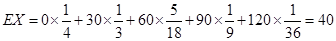 ��
��
��������������Ҫ�����˹ŵ���͡����θ��ͣ��ŵ�����õ���֪ʶ��Ϊ������=������������������֮�ȣ��ŵ�����뼸�θ��͵���Ҫ�������ڣ����θ�������һ��ȿ��ܸ��ͣ�����ŵ���͵�������������Ľ���������������θ��͵��ص���������������1�����������п��ܳ��ֵĻ����¼������������2��ÿ�������¼����ֵĿ�������ȣ�
��I���衰����Ż�ȯ��Ϊ�¼�A����Ϊ�ٶ�ָ��ͣ����һλ�ö��ǵȿ��ܵģ������������������ֵ������ȣ��ʱ�С�����ü��θ�����⼴�ɣ�
��II���衰�һ���Ż�ȯ������20Ԫ��Ϊ�¼�B����Ϊ�˿���ת����ת�����Σ����ҵ�һ��ת��ת�̻���Ż�ȯ���ΪxԪ��
�ڶ��λ���Ż�ȯ���ΪyԪ��������¼��ռ���Ա�ʾΪ����={��20��20������20��10������20��0������10��20������10��10������10��0������0��20������0��10������0��0��}�����������ʱ�С�����ùŵ������⣮
�⣺(��)��ָ������A,B,C����ֱ��Ϊ�¼�A,B,C.
��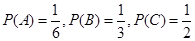 ������������3��
������������3��
����ȯ������30Ԫ����ָ������A��B����.
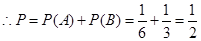 ��������������5��
��������������5��
������128Ԫ�Ĺ˿ͣ���ȯ������30Ԫ�ĸ�����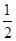 .
.
����������ã��ù˿Ϳ�ת��ת��2��.
�������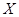 �Ŀ���ֵΪ0��30��60��90��120. ��������������6��
�Ŀ���ֵΪ0��30��60��90��120. ��������������6��
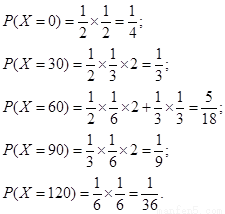 ����������������9��
����������������9��
���ԣ��������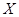 �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
0 |
30 |
60 |
90 |
120 |
||
|
|
|
|
|
|
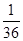
|
����ѧ����
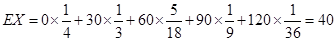 ������������������12��
������������������12��