Question

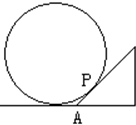（2006•丰台区二模）如图，水平地面上有一个大球，现有如下方法测量球的大小：用一个锐角为45°的三角板，斜边紧靠球面，一条直角边紧靠地面，并使三角板与地面垂直，P为三角板与球的切点，如果测得PA=2，则球的表面积为

(48+32

2

)π

．

Answer 1

分析：设球与地面的切点为B，球心为O，连结OA、OB、OP．由切线的性质和四边形ABOP内角和定理，算出∠POB=45°，因此△POA中，可得∠POA=

1

2

×45°=22.5°．由正切的定义在Rt△POA中算出OP=

PA

tan22.5°

=2+2

2

，得球半径R=2+2

2

，再利用球表面积公式可算出答案．

解答：解：设球与地面的切点为B，球心为O，连结OA、OB、OP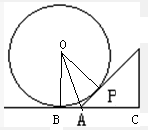
∵四边形ABOP中，OP⊥AP，OB⊥AB
∴∠POB=180°-∠PAB=∠PAC=45°
因此，△POA中∠POA=

1

2

×45°=22.5°
Rt△POA中，tan∠POA=

PA

OP

，得OP=

PA

tan22.5°

=

2

2 -1

=2+2

2

即球的半径R=2+2

2

，得球的表面积为
S=4πR²=4π×（2+2

2

）²=(48+32

2

)π
故答案为：(48+32

2

)π

点评：本题给出球与等腰直角三角板相切，在已知切点到等腰直角三角形的顶点的距离情况下，求球的表面积．着重考查了切线的性质、四边形ABOP内角和定理、球的表面积公式等知识，属于中档题．