题目内容
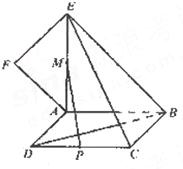 如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°(I)求证:EF⊥平面BCE;
(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
(Ⅲ)求二面角F-BD-A的大小.
分析:(1)欲证EF⊥平面BCE,根据线面垂直的判定定理可知只需证EF⊥BE,BC⊥EF,BC∩BE=B,根据条件很显然;
(2)取BE的中点N,连接CN,MN,易证PM∥CN,根据线面平行的判定定理很快得证;
(3)作FG⊥AB,交BA的延长线于G,作GH⊥BD于H,连接FH,易证∠FHG为二面角F-BD-A的平面角,在Rt△FGH中求出此角即可.
(2)取BE的中点N,连接CN,MN,易证PM∥CN,根据线面平行的判定定理很快得证;
(3)作FG⊥AB,交BA的延长线于G,作GH⊥BD于H,连接FH,易证∠FHG为二面角F-BD-A的平面角,在Rt△FGH中求出此角即可.
解答: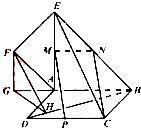 解:因为平面ABEF⊥平面ABCD,BC?平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
解:因为平面ABEF⊥平面ABCD,BC?平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF
所以BC⊥EF
因为△ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE
因为BC?平面ABCD,BE?平面BCE,
BC∩BE=B
所以EF⊥平面BCE
( II)取BE的中点N,连接CN,MN,则MN=
AB=PC
∴PMNC为平行四边形,所以PM∥CN
∵CN在平面BCE内,PM不在平面BCE内,
∴PM∥平面BCE.
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD、
作FG⊥AB,交BA的延长线于G,则FG∥EA、从而FG⊥平面ABCD,
作GH⊥BD于H,连接FH,则由三垂线定理知BD⊥FH、
∴∠FHG为二面角F-BD-A的平面角、
∵FA=FE,∠AEF=45°,
∠AEF=90°,∠FAG=45°、
设AB=1,则AE=1,AF=
,则FG=AF•sinFAG=
在Rt△BGH中,∠GBH=45°,BG=AB+AG=1+
=
,
GH=BG•sinGBH=
•
=
,
在Rt△FGH中,tanFHG=
=
,
∴二面角F-BD-A的大小为arctan
 解:因为平面ABEF⊥平面ABCD,BC?平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
解:因为平面ABEF⊥平面ABCD,BC?平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,所以BC⊥平面ABEF
所以BC⊥EF
因为△ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE
因为BC?平面ABCD,BE?平面BCE,
BC∩BE=B
所以EF⊥平面BCE
( II)取BE的中点N,连接CN,MN,则MN=
| 1 |
| 2 |
∴PMNC为平行四边形,所以PM∥CN
∵CN在平面BCE内,PM不在平面BCE内,
∴PM∥平面BCE.
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD、
作FG⊥AB,交BA的延长线于G,则FG∥EA、从而FG⊥平面ABCD,
作GH⊥BD于H,连接FH,则由三垂线定理知BD⊥FH、
∴∠FHG为二面角F-BD-A的平面角、
∵FA=FE,∠AEF=45°,
∠AEF=90°,∠FAG=45°、
设AB=1,则AE=1,AF=
| ||
| 2 |
| 1 |
| 2 |
在Rt△BGH中,∠GBH=45°,BG=AB+AG=1+
| 1 |
| 2 |
| 3 |
| 2 |
GH=BG•sinGBH=
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
在Rt△FGH中,tanFHG=
| FG |
| GH |
| ||
| 3 |
∴二面角F-BD-A的大小为arctan
| ||
| 3 |
点评:本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为