题目内容
(本小题满分12分)已知f (x)=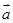 ·
·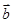 -1,其中向量
-1,其中向量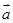 =(
=( sin2x,cosx),
sin2x,cosx),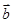 =(1,2cosx)(x∈R)
=(1,2cosx)(x∈R)
(Ⅰ)求f (x)的单调递减区间;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a、b、c,f (A)=2,a=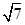 ,b=
,b= ,
,
求边长c的值。
【答案】
解⑴f (x)=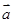 ·
·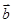 -1=(
-1=(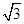 sin2x,cosx)·(1,2cosx)-1
sin2x,cosx)·(1,2cosx)-1
=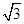 sin2x+2cos2x-1
…………1分
sin2x+2cos2x-1
…………1分
=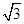 sin2x+cos2x
…………2分
sin2x+cos2x
…………2分
=2sin(2x+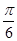 )
…………4分
)
…………4分
由2kπ+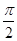 ≤2x+
≤2x+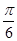 ≤2kπ+
≤2kπ+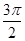 得
kπ+
得
kπ+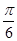 ≤x≤kπ+
≤x≤kπ+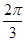
∴f (x)的递减区间为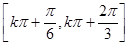 (k∈z) …………6分
(k∈z) …………6分
⑵ f (A)=2sin(2A+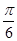 )=2 ∴sin(2A+
)=2 ∴sin(2A+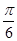 )=1 ………7分
)=1 ………7分
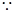
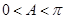 ∴
∴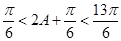 ∴2A+
∴2A+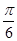 =
=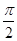
∴A=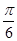 …………………………………8分
…………………………………8分
由余弦定理得 a2=b2+c2-2bccosA
7=3+c2―3c 即 c2―3c―4=0 …………9分
(c-4)(c+1)=0 … 10分
∴c=4或c=―1 (不合题意,舍去) ……11分
∴c=4 ………12分
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目