Question

设f(x)=ax³+bx²+cx，其导函数y=f′(x)的图像经过点(-2，0)，(，0)，且f(x)在x=-2时取得极小值-8．

(Ⅰ)求f(x)的解析式；

(Ⅱ)若对x∈[-3，3]都有f(x)≥m²-14m恒成立，求实数m的取值范围．

Answer 1

解：(1)∵f′(x)=3ax²+2bx+c,

且y=f′(x)的图像经过点(-2，0)，(，0)，

∴，

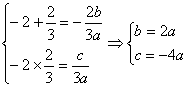∴f(x)=ax³+2 ax²-4ax，

由f(x)_极小值=f(-2)=a(-2)³+2a(-2)²-4a(-2)=-8，解得a=-1

∴f(x)=-x³-2x²+4，

(Ⅱ)要使对x∈[-3，3]都有f(x)≥m²-14m恒成立，

只需f(x)_min≥m²-14m即可．

∵f′(x)=-3x²-4x+4=-2(x-)(x+2)

∴函数y=f(x)在[-3，-2)上单调递减，在(-2，)上单调递增，在(，3)上单调递减，

又∵f(-2)=-8，

f(3)=-3³-2×3²+4×3=-33＜-8，

∴f(x)_min=f(3)=-33

-33≥m²-14m3≤m≤11

故所求的实数m的取值范围为{m|3≤m≤11}．