题目内容
已知a,b,c均为正数,且都不等于1,若实数x,y,z满足ax=by=cz,
+
+
=0,则abc的值等于( )
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
分析:由题意设ax=by=cz=k(k>0),则x=logak,y=logbk,z=logck,再由
+
+
=logka+logkb+logkc=logkabc=0,能求出abc=1.
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
解答:解:∵a,b,c均为正数,且都不等于1,
实数x,y,z满足ax=by=cz,
+
+
=0,
∴设ax=by=cz=k(k>0),
则x=logak,y=logbk,z=logck,
∴
+
+
=logka+logkb+logkc=logkabc=0,
∴abc=1.
故选A.
实数x,y,z满足ax=by=cz,
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
∴设ax=by=cz=k(k>0),
则x=logak,y=logbk,z=logck,
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
∴abc=1.
故选A.
点评:本题考查对数函数的性质和换底公式的应用,解题时要认真审题,仔细解答,注意换底公式的灵活运用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
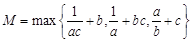 ,则M的最小值为 .
,则M的最小值为 .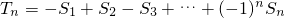 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;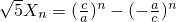 (n∈N+),证明:数列{
(n∈N+),证明:数列{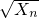 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.