题目内容
已知a,b,c均为正实数,记M=max{
+b,
+bc,
+c},则M的最小值为
| 1 |
| ac |
| 1 |
| a |
| a |
| b |
2
2
.分析:先根据c的范围,讨论第一个数和第二个数的大小关系.在每种情况中分别用均值不等式和不等式的性质确定M的范围,即可得解
解答:解:由题意知M≥
+b>0,M≥
+bc>0,M≥
+c>0
∵(
+b)c=
+bc>0
①当c≥1时,
+bc≥
+b>0
∴只需考虑M≥
+bc,M≥
+c
∴M≥
+bc≥
+b≥2
,M≥
+c≥
+1≥2
∴M2≥2
×2
=4
∴M≥2,当a=b=c=1时取等号
②当c<1时,0<
+bc<
+b,只需考虑M≥
+b,M≥
+c
∴M2≥(
+b)(
+c)=a+
+
+bc≥2
+2
=4
∴M≥2
∴M的最小值为2
故答案为:2
| 1 |
| ac |
| 1 |
| a |
| a |
| b |
∵(
| 1 |
| ac |
| 1 |
| a |
①当c≥1时,
| 1 |
| a |
| 1 |
| ac |
∴只需考虑M≥
| 1 |
| a |
| a |
| b |
∴M≥
| 1 |
| a |
| 1 |
| a |
|
| a |
| b |
| a |
| b |
|
∴M2≥2
|
|
∴M≥2,当a=b=c=1时取等号
②当c<1时,0<
| 1 |
| a |
| 1 |
| ac |
| 1 |
| ac |
| a |
| b |
∴M2≥(
| 1 |
| ac |
| a |
| b |
| 1 |
| a |
| 1 |
| bc |
a×
|
|
∴M≥2
∴M的最小值为2
故答案为:2
点评:本题考查不等式不比较大小,同时考查均值不等式和不等式的性质,须特别注意同向不等式的应用和均值不等式的条件.属中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
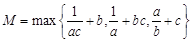 ,则M的最小值为 .
,则M的最小值为 .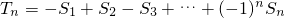 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;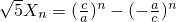 (n∈N+),证明:数列{
(n∈N+),证明:数列{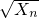 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.