题目内容
已知直角△ABC的三边长a,b,c,满足a≤b<c
(1)在a,b之间插入2011个数,使这2013个数构成以a为首项的等差数列{an },且它们的和为2013,求c的最小值;
(2)已知a,b,c均为正整数,且a,b,c成等差数列,将满足条件的三角形的面积从小到大排成一列S1,S2,S3,…Sn,且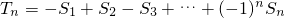 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;
(3)已知a,b,c成等比数列,若数列{Xn}满足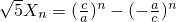 (n∈N+),证明:数列{
(n∈N+),证明:数列{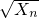 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
(1)解:{an}是等差数列,∴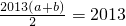 ,即a+b=2.
,即a+b=2.
所以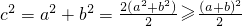 =
=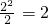 ,
,
所以c的最小值为 ;
;
(2)解:设a,b,c的公差为d(d∈Z),则a2+(a+d)2=(a+2d)2
∴a=3d.
设三角形的三边长为3d,4d,5d,面积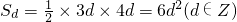 ,则
,则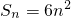 ,
,
T2n=-S1+S2-S3+…+S2n
=6[-12+22-32+42-…+(2n)2]
=6(1+2+3+4+…+2n)=12n2+6n.
由 得
得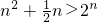 ,
,
当n≥5时,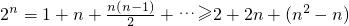 >
>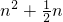 ,
,
经检验当n=2,3,4时,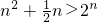 ,当n=1时,
,当n=1时,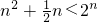 .
.
综上所述,满足不等式 的所有n的值为2、3、4.
的所有n的值为2、3、4.
(3)证明:因为a,b,c成等比数列,∴b2=ac.
由于a,b,c为直角三角形的三边长,知a2+ac=c2,∴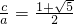 ,
,
又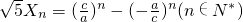 ,得
,得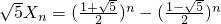 ,
,
于是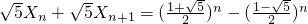
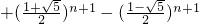
=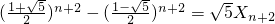 .
.
∴Xn+Xn+1=Xn+2,则有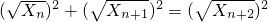 .
.
故数列{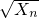 }中的任意连续三项为边长均可以构成直角三角形.
}中的任意连续三项为边长均可以构成直角三角形.
因为
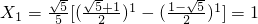 ,
,
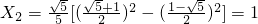 ,
,
?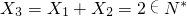 ,
,
由Xn+Xn+1=Xn+2,同理可得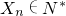 ,
,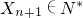 ?Xn+2∈N*,
?Xn+2∈N*,
故对于任意的n∈N*都有Xn是正整数.
分析:(1)由等差数列的前2013项的和求出a+b的值,利用勾股定理写出c2=a2+b2,然后利用基本不等式求c的最小值;
(2)设出三角形三边的公差,由勾股定理求得三边与公差的关系,把面积用公差表示,则Sn可求,把Sn代入
T2n=-S1+S2-S3+…+S2n后,先裂项后利用等差数列求和公式求和,得到Tn后结合二项展开式的系数和取值验证求得满足不等式 的所有n的值;
的所有n的值;
(3)由a,b,c成等比数列,结合直角三角形中边的关系求出 ,代入
,代入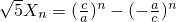 后整理,进一步得到
后整理,进一步得到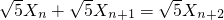 ,由此可证数列{
,由此可证数列{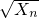 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
点评:本题以直角三角形边的关系为载体,考查了等差数列的前n项和公式,考查了利用基本不等式求最值,考查了用裂项法求数列的和,训练了利用二项展开式的二项式系数比较不等式的大小,此题综合性强,难度较大.
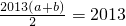 ,即a+b=2.
,即a+b=2.所以
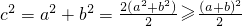 =
=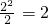 ,
,所以c的最小值为
 ;
;(2)解:设a,b,c的公差为d(d∈Z),则a2+(a+d)2=(a+2d)2
∴a=3d.
设三角形的三边长为3d,4d,5d,面积
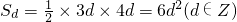 ,则
,则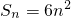 ,
,T2n=-S1+S2-S3+…+S2n
=6[-12+22-32+42-…+(2n)2]
=6(1+2+3+4+…+2n)=12n2+6n.
由
 得
得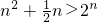 ,
,当n≥5时,
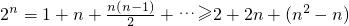 >
>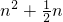 ,
,经检验当n=2,3,4时,
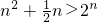 ,当n=1时,
,当n=1时,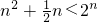 .
.综上所述,满足不等式
 的所有n的值为2、3、4.
的所有n的值为2、3、4.(3)证明:因为a,b,c成等比数列,∴b2=ac.
由于a,b,c为直角三角形的三边长,知a2+ac=c2,∴
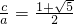 ,
,又
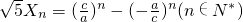 ,得
,得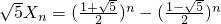 ,
,于是
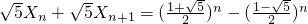
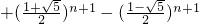
=
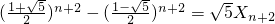 .
.∴Xn+Xn+1=Xn+2,则有
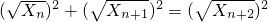 .
.故数列{
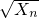 }中的任意连续三项为边长均可以构成直角三角形.
}中的任意连续三项为边长均可以构成直角三角形.因为
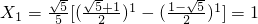 ,
,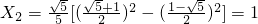 ,
,?
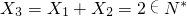 ,
,由Xn+Xn+1=Xn+2,同理可得
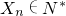 ,
,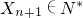 ?Xn+2∈N*,
?Xn+2∈N*,故对于任意的n∈N*都有Xn是正整数.
分析:(1)由等差数列的前2013项的和求出a+b的值,利用勾股定理写出c2=a2+b2,然后利用基本不等式求c的最小值;
(2)设出三角形三边的公差,由勾股定理求得三边与公差的关系,把面积用公差表示,则Sn可求,把Sn代入
T2n=-S1+S2-S3+…+S2n后,先裂项后利用等差数列求和公式求和,得到Tn后结合二项展开式的系数和取值验证求得满足不等式
 的所有n的值;
的所有n的值;(3)由a,b,c成等比数列,结合直角三角形中边的关系求出
 ,代入
,代入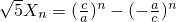 后整理,进一步得到
后整理,进一步得到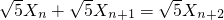 ,由此可证数列{
,由此可证数列{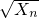 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.点评:本题以直角三角形边的关系为载体,考查了等差数列的前n项和公式,考查了利用基本不等式求最值,考查了用裂项法求数列的和,训练了利用二项展开式的二项式系数比较不等式的大小,此题综合性强,难度较大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 相交于D、E两点,△CDE是以C(2,5)为直角顶点的等腰直角三角形,求该椭圆的方程.
相交于D、E两点,△CDE是以C(2,5)为直角顶点的等腰直角三角形,求该椭圆的方程.