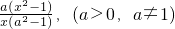题目内容
设f(logax)=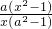
(1)求f(x)的表达式,并判断f(x)的奇偶性;
(2)试证明:函数f(x)的图象上任意两点的连线的斜率大于0;
(3)对于f(x),当x∈(-1,1)时,恒有f(1-m)+f(1-m2)<0求m的取值范围.
解:(1)令t=logax( t∈R),可得 x=at,代入f(logax)=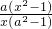 中,得 f(t)=
中,得 f(t)= (
( 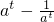 ),
),
∴f(x)= (
( ),
),
f(x)的定义域为R,关于原点对称,且f(-x)= (
(  )=-
)=- (
( )=-f(x),故f(x)为奇函数.
)=-f(x),故f(x)为奇函数.
(2)当a>1时, >0,
>0, 为增函数,故 f(x)=
为增函数,故 f(x)= (
( ) 在R上是增函数.
) 在R上是增函数.
当 0<a<1时, <0,
<0, 为减函数,故 f(x)=
为减函数,故 f(x)= (
( ) 在R上是增函数.
) 在R上是增函数.
综上,f(x)为增函数,由增函数的定义知:对任意x1<x2,有 f(x1)<f(x2),∴ >0,
>0,
故任意两点的连线斜率都大于零.
(3)由(1)知f(x)为奇函数,由(2)知f(x)在(-1,1)上为增函数,
故有-1<1-m<m2-1<1,解得 1<m< ,即m的取值范围为(1,
,即m的取值范围为(1, ).
).
分析:(1)用换元法求函数的解析式,再根据函数的奇偶性的定义判断函数f(x)为奇函数.
(2)分当a>1时和 0<a<1时两种情况,根据 的符号以及
的符号以及 的单调性,判断f(x)的单调性,从而得出结论.
的单调性,判断f(x)的单调性,从而得出结论.
(3)根据f(x)为奇函数,在(-1,1)上为增函数,可得-1<1-m<m2-1<1,由此求得m的取值范围.
点评:本题主要考查用换元法求函数的解析式,函数的奇偶性和单调性的应用,直线的斜率公式,体现了分类讨论的数学思想,属于中档题.
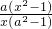 中,得 f(t)=
中,得 f(t)= (
( 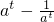 ),
),∴f(x)=
 (
( ),
),f(x)的定义域为R,关于原点对称,且f(-x)=
 (
(  )=-
)=- (
( )=-f(x),故f(x)为奇函数.
)=-f(x),故f(x)为奇函数.(2)当a>1时,
 >0,
>0, 为增函数,故 f(x)=
为增函数,故 f(x)= (
( ) 在R上是增函数.
) 在R上是增函数.当 0<a<1时,
 <0,
<0, 为减函数,故 f(x)=
为减函数,故 f(x)= (
( ) 在R上是增函数.
) 在R上是增函数.综上,f(x)为增函数,由增函数的定义知:对任意x1<x2,有 f(x1)<f(x2),∴
 >0,
>0,故任意两点的连线斜率都大于零.
(3)由(1)知f(x)为奇函数,由(2)知f(x)在(-1,1)上为增函数,
故有-1<1-m<m2-1<1,解得 1<m<
 ,即m的取值范围为(1,
,即m的取值范围为(1, ).
).分析:(1)用换元法求函数的解析式,再根据函数的奇偶性的定义判断函数f(x)为奇函数.
(2)分当a>1时和 0<a<1时两种情况,根据
 的符号以及
的符号以及 的单调性,判断f(x)的单调性,从而得出结论.
的单调性,判断f(x)的单调性,从而得出结论.(3)根据f(x)为奇函数,在(-1,1)上为增函数,可得-1<1-m<m2-1<1,由此求得m的取值范围.
点评:本题主要考查用换元法求函数的解析式,函数的奇偶性和单调性的应用,直线的斜率公式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目