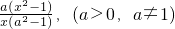Question

设f（log_ax）=

a(x2-1)

x(a2-1)

，(a＞0，a≠1)
求证：
（1）过函数y=f（x）图象上任意两点直线的斜率恒大于0；
（2）f（3）＞3．

Answer 1

证明：（1）令t=log_ax，则x=a^t，f（t）=

a

a2-1

(at-a-t)（t∈R），
∴f（x）=

a

a2-1

(ax-a-x)（x∈R），
设x₁＜x₂，f（x₁）-f（x₂）=

a(ax1-ax2)(ax1+x2+1)

(a2-1)ax1+x2

，
（1）当a＞1时，因为x₁0，ax1-ax2＜0，
所以f（x₁）-f（x₂）＜0，即f（x₁）＜f（x₂），
∴f（x）在（-∞，+∞）上单调递增；
（2）当0＜a＜1时，因为a²-1＜0，ax1-ax2＞0，
所以f（x₁）-f（x₂）＜0，即f（x₁）＜f（x₂），
∴f（x）在（-∞，+∞）上单调递增；
∴x₁＜x₂时，恒有f（x₁）＜f（x₂），∴K=

f(x1)-f(x2)

x1-x2

＞0，
故过函数y=f（x）图象上任意两点直线的斜率恒大于0；
（2）f（3）=

a

a2-1

(a3-a-3)=

a(a6-1)

a3(a2-1)

=

a4+a2+1

a2

=a2+

1

a2

+1≥2

a2• 1 a2

+1=3，
∵a＞0，a≠1，∴a2≠

1

a2

，∴上述不等式不能取等号，
∴f（3）＞3．