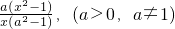题目内容
设f(logax)=
求证:
(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;
(2)f(3)>3.
【答案】分析:(1)先用换元法求出函数f(x)的解析式,要证过函数y=f(x)图象上任意两点直线的斜率恒大于0,只需证明函数f(x)为增函数即可,用单调性定义可证明;
(2)代入解析式化简可得,f(3)=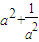 +1,运用基本不等式即可证明,注意等号不等取到;
+1,运用基本不等式即可证明,注意等号不等取到;
解答:证明:(1)令t=logax,则x=at,f(t)=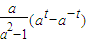 (t∈R),
(t∈R),
∴f(x)= (x∈R),
(x∈R),
设x1<x2,f(x1)-f(x2)=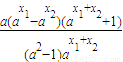 ,
,
(1)当a>1时,因为x10,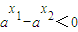 ,
,
所以f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-∞,+∞)上单调递增;
(2)当0<a<1时,因为a2-1<0,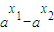 >0,
>0,
所以f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-∞,+∞)上单调递增;
∴x1<x2时,恒有f(x1)<f(x2),∴K= >0,
>0,
故过函数y=f(x)图象上任意两点直线的斜率恒大于0;
(2)f(3)=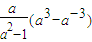 =
=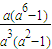 =
=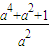 =
=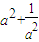 +1≥2
+1≥2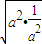 +1=3,
+1=3,
∵a>0,a≠1,∴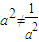 ,∴上述不等式不能取等号,
,∴上述不等式不能取等号,
∴f(3)>3.
点评:本题考查函数解析式的求法,考查单调性的判断及直线斜率问题,考查基本不等式的应用,具有一定综合性,属中档题.
(2)代入解析式化简可得,f(3)=
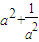 +1,运用基本不等式即可证明,注意等号不等取到;
+1,运用基本不等式即可证明,注意等号不等取到;解答:证明:(1)令t=logax,则x=at,f(t)=
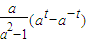 (t∈R),
(t∈R),∴f(x)=
 (x∈R),
(x∈R),设x1<x2,f(x1)-f(x2)=
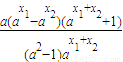 ,
,(1)当a>1时,因为x10,
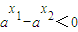 ,
,所以f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-∞,+∞)上单调递增;
(2)当0<a<1时,因为a2-1<0,
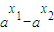 >0,
>0,所以f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-∞,+∞)上单调递增;
∴x1<x2时,恒有f(x1)<f(x2),∴K=
 >0,
>0,故过函数y=f(x)图象上任意两点直线的斜率恒大于0;
(2)f(3)=
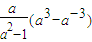 =
=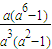 =
=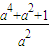 =
=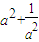 +1≥2
+1≥2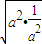 +1=3,
+1=3,∵a>0,a≠1,∴
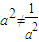 ,∴上述不等式不能取等号,
,∴上述不等式不能取等号,∴f(3)>3.
点评:本题考查函数解析式的求法,考查单调性的判断及直线斜率问题,考查基本不等式的应用,具有一定综合性,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目