题目内容
已知a，b，c是半径为1的圆内接△ABC的三边，且S△ABC=1，则以sinA，sinB，sinC为三边组成的三角形的面积为 ．
【答案】分析：由正弦定理可得，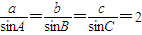
可得
a=sinA，
b=sinB，
c=sinC，则以sinA，sinB，sinC为三边组成的三角形的面积为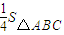
解答：解：由正弦定理可得，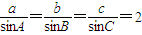
a=sinA，
b=sinB，
c=sinC
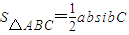=1
则以sinA，sinB，sinC为三边组成的三角形的面积为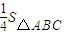
=
故答案为：
点评：本题主要考查了正弦定理，三角形的面积公式的应用，属于公式的简单应用．
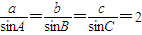可得a=sinA，b=sinB，c=sinC，则以sinA，sinB，sinC为三边组成的三角形的面积为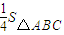解答：解：由正弦定理可得，
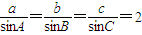
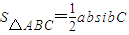a=sinA，b=sinB，c=sinC=1则以sinA，sinB，sinC为三边组成的三角形的面积为
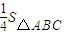=故答案为：
点评：本题主要考查了正弦定理，三角形的面积公式的应用，属于公式的简单应用．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目