题目内容
已知抛物线C:y2=2px(p>0)的准线与直线l:y=k(x+2)(k≠0)的交点M在x轴上,直线l与抛物线C交于不同的两点A,B,线段AB的垂直平分线交x轴于点N(t,0).
(Ⅰ)求抛物线C的方程;
(Ⅱ)求实数t的取值范围;
(Ⅲ)若抛物线C的焦点和准线分别为椭圆Q的左焦点和左准线,试求椭圆Q的短轴端点的轨迹方程.
答案:
解析:
解析:
解:(Ⅰ)∵准线与直线l交点在x轴上,交点为![]() ,且直线过定点
,且直线过定点![]()
∴![]() ,即
,即![]()
∴抛物线方程为![]() 4分;
4分;
(Ⅱ)由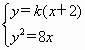 得
得![]()
![]() ∴
∴![]() 且
且![]() 5分
5分
![]() 6分
6分
∴![]() 的中垂线方程为
的中垂线方程为![]() ,令
,令![]() ,得
,得![]() 7分
7分
![]() 8分;
8分;
(Ⅲ)∵抛物线焦点F(2,0),准线![]() ,∴
,∴![]() 是抛物线
是抛物线![]() 的左准线
的左准线
设Q的中心为![]()
![]() ,则短轴端点为
,则短轴端点为![]() 10分
10分
∵F为左焦点,则![]() ,
,![]() ∴
∴![]()
依左准线方程有![]() 12分
12分
![]() 即
即![]() 14分
14分

练习册系列答案
相关题目


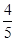 B.
B. C.-
C.-