题目内容
已知函数y=sin2x+acos2x的图像关于直线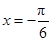 对称,则函数y=asin2x-cos2x的图象关于下列各点中对称的是( )
对称,则函数y=asin2x-cos2x的图象关于下列各点中对称的是( )
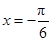 对称,则函数y=asin2x-cos2x的图象关于下列各点中对称的是( )
对称,则函数y=asin2x-cos2x的图象关于下列各点中对称的是( )A.(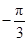 ,0) ,0) | B.(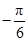 ,0) ,0) | C.(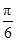 ,0) ,0) | D.(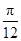 ,0) ,0) |
B
分析:利用辅助角公式化简函数的表达式为一个角的一个三角函数的形式,结合提交求出θ,然后化简函数y=asin2x-cos2x求出对称中心即可.
解答:解:函数y=sin2x+acos2x= sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线x=-
sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线x=-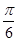 对称,所以θ=kπ+
对称,所以θ=kπ+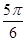 ,k∈Z,
,k∈Z,
则函数y=asin2x-cos2x=- cos(2x+θ),显然x=-
cos(2x+θ),显然x=-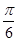 时,cos(2x+θ)=0,就是函数关于(-
时,cos(2x+θ)=0,就是函数关于(-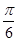 ,0)对称;
,0)对称;
故选B
解答:解:函数y=sin2x+acos2x=
 sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线x=-
sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线x=-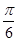 对称,所以θ=kπ+
对称,所以θ=kπ+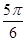 ,k∈Z,
,k∈Z,则函数y=asin2x-cos2x=-
 cos(2x+θ),显然x=-
cos(2x+θ),显然x=-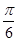 时,cos(2x+θ)=0,就是函数关于(-
时,cos(2x+θ)=0,就是函数关于(-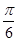 ,0)对称;
,0)对称;故选B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,记
,记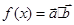 ,要得到函数
,要得到函数 的图像,只须将
的图像,只须将 的图像()
的图像()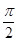 个单位 B 向右平移
个单位 B 向右平移 个单位 D向右平移
个单位 D向右平移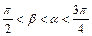 ,
,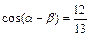 ,
,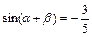 ,
,

 求f(x)解析式及单调递增区间.
求f(x)解析式及单调递增区间.
 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.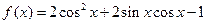 .
.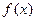 的最小正周期;
的最小正周期;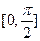 上的最大值与最小值.
上的最大值与最小值.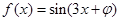 的图象关于直线
的图象关于直线 对称,则
对称,则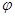 的最小正值等于( )
的最小正值等于( ) 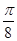
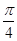
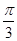
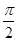
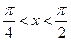 ,则函数
,则函数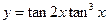 的最大值为 .
的最大值为 .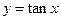 在定义域上单调递增;
在定义域上单调递增;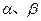 满足
满足 ,则
,则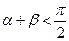 ;
;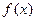 是定义在
是定义在 上的偶函数,且在
上的偶函数,且在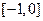 上是增函数,若
上是增函数,若 则
则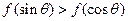 ;
; 的图象,只需将
的图象,只需将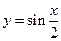 的图象向左平移
的图象向左平移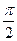 个单位;
个单位; 2分)
2分)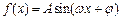 (
(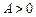 ,
, ,
,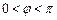
 )在
)在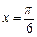 取得最大值2,方程
取得最大值2,方程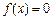 的两个根为
的两个根为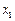 、
、 ,且
,且 的最小值为
的最小值为 .
. ;
; 图象上各点的横坐标压缩到原来的
图象上各点的横坐标压缩到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数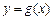 的图象.当
的图象.当 时,函数
时,函数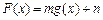 (m、n∈R)的值域是
(m、n∈R)的值域是 ,求实数m、n的值.
,求实数m、n的值.