题目内容
已知向量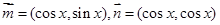 ,设函数
,设函数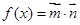
(I)求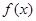 的解析式,并求最小正周期;
的解析式,并求最小正周期;
(II)若函数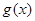 的图像是由函数
的图像是由函数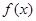 的图像向右平移
的图像向右平移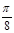 个单位得到的,求
个单位得到的,求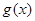 的最大值及使
的最大值及使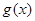 取得最大值时
取得最大值时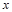 的值.
的值.
【答案】
(I)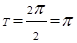 ; (II)
; (II)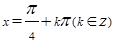 时,
时,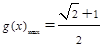
【解析】
试题分析:(I)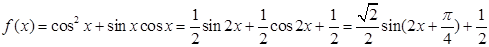 (
(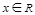 )
)
故最小正周期为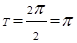
(II)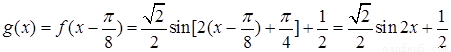
故当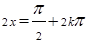 ;即
;即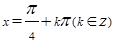 时,
时,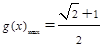
考点:平面向量的坐标运算,和差倍半的三角函数公式,正弦型函数图象的变换,三角函数的图像和性质。
点评:典型题,本题综合性较强,利用三角公式,将研究对象“化一”,是高考要求的基本问题,在此基础上,进一步研究函数的图象和性质。函数图象的平移遵循“左加右减,上加下减”。

练习册系列答案
相关题目

 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像. ,设函数
,设函数 ;
; 求函数f(x)的最值及对应的x的值;-
求函数f(x)的最值及对应的x的值;- 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,设函数
,设函数 .
. ,求f(A+B)的值.
,求f(A+B)的值. ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.