题目内容
对于函数f(x),如果有限集合S满足:①S⊆N*;②当x∈S时,f(x)∈S,则称集合S是函数f(x)的生成集.例如f(x)=4-x,那么集合S1={2},S2={1,3},S3={1,2,3}都是f(x)的生成集,对于f(x)=
(x>2,a,b∈R,若f(x)是减函数,S是f(x)的生成集,则S不可能是( )
| ax+b |
| x-2 |
| A、{3,4,5,6,8,14} |
| B、{3,4,6,10,18} |
| C、{3,5,6,7,10,16} |
| D、{3,4,6,7,12,22} |
分析:利用生成集的意义和减函数的意义即可判断出.
解答:解:对于A:假设S是f(x)的生成集,又f(x)是减函数,
∴
,解得
,可得f(x)=
,
验证:f(5)=
=6,f(6)=
=5,f(8)=
=4,f(14)=
=3.
因此:S是f(x)的生成集.故假设正确.
同理对于B,D也正确.
对于C:假设S是f(x)的生成集,又f(x)是减函数,
∴
,解得
,∴f(x)=
,
验证:f(6)=
=
∉S,因此假设不正确,故S不是f(x)的生成集.
综上可知:只有A,B,D正确.
故选:C.
∴
|
|
| 2x+8 |
| x-2 |
验证:f(5)=
| 2×5+8 |
| 5-2 |
| 2×6+8 |
| 6-2 |
| 2×8+8 |
| 8-2 |
| 2×14+8 |
| 14-2 |
因此:S是f(x)的生成集.故假设正确.
同理对于B,D也正确.
对于C:假设S是f(x)的生成集,又f(x)是减函数,
∴
|
|
| 7x-5 |
| x-2 |
验证:f(6)=
| 7×6-5 |
| 6-2 |
| 37 |
| 4 |
综上可知:只有A,B,D正确.
故选:C.
点评:本题考查了“生成集”的意义、减函数的意义,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
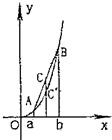 如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,
如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方, 如图,对于函数f(x)=x2(x>0)的图象上不同两点A(a,a2)、B(b,b2),直线段AB
如图,对于函数f(x)=x2(x>0)的图象上不同两点A(a,a2)、B(b,b2),直线段AB 下列4个命题:
下列4个命题: